Многим термин абсолютная величина наводит скуку, так как в связи с этим зачастую
приходится рассматривать большое количество случаев, в которых не мудрено запутаться. Скажу откровенно, что полностью
исключить перебор не всегда получается, но если подойти к задаче творчески, количество возможных случаев удается свести к минимуму.
Абсолютную величину часто называют модулем. Действительно это слово короче писать и произносить,
но мы все же предпочитаем оставить слово «модуль» для комплексных чисел.
Абсолютная величина использовалась еще в XVI веке шотландским математиком Джоном Непером (John Napier) для создания первых в мире таблиц логарифмов. Самое ранее известное употребление термина «абсолютная величина» относится к 1806 году в трудах графа Карно (Lazare Nicolas M. Carnot), который также ввел в употребление термин «комплексное число». Термин «модуль» ввел в употребление другой французский математик Жан-Робер Арган (Jean-Robert Argand) в том же 1806 году. Обозначение $|...|$ изобрел знаменитый Карл Вейерштрасс (Karl Weierstraß) в 1841 году.
1. Абсолютная величина и ее свойства.
1.1 Определение и основные свойства абсолютной величины.
Следуя точно по учебнику, для определения абсолютной величины следует рассмотреть три возможных случая,
когда выражение под знаком абсолютной величины |...| положительно, нуль или отрицательно:
$$
|a| =
\begin{cases}
\mathtt\;\;\, a,\quad если\quad a \gt 0, \\
\mathtt\;\;\, 0,\quad если\quad a = 0, \\
\mathtt-a,\quad если\quad a \lt 0
\end{cases}\label{eq:1.1.1}\tag{1.1.1}
$$
Для практических целей удобнее объединить первые два случая:
$$
|a| =
\begin{cases}
\mathtt\;\;\, a,\quad если\quad a \geqslant 0, \\
\mathtt-a,\quad если\quad a \lt 0
\end{cases} \label{eq:1.1.1a}\tag{1.1.1a}
$$
Как наверное помнят даже те, кто забыли многое из того, что проходили в школе, абсолютная величина всегда неотрицательна
$$
|a| \geqslant 0 \label{eq:1.1.2}\tag{1.1.2}
$$
что вытекает непосредственно из определения абсолютной величины.
Отметим другое, не менее важное свойство, также доказываемое непосредственно: абсолютные величины противоположных чисел равны:
$$
|-a| = |a| \label{eq:1.1.3}\tag{1.1.3}
$$
Можно определение абсолютной величины записать в одну строку, если воспользоваться обозначением $max$, то есть максимум или наибольшее значение:
$$
|a| = max(a,-a) \label{eq:1.1.4}\tag{1.1.4}
$$
Если бы не устоявшаяся традиция, равенство $\eqref{eq:1.1.4}$ можно было бы также принять в качестве определения абсолютной величины. В таком случае $\eqref{eq:1.1.1}$ становится одним из свойств.
Наряду с абсолютной величиной числа удобно рассматривать «отрицательную абсолютную величину $-|a|$. В то время как абсолютная величина числа всегда неотрицательна, «отрицательная абсолютная величина» заведомо неположительна:
$$
-|a| \leqslant 0 \label{eq:1.1.2a}\tag{1.1.2a}
$$
Равенство $\eqref{eq:1.1.4}$ также можно «перефразировать» для «отрицательной абсолютной величины»:
$$
-|a| = min(a,-a) \label{eq:1.1.4a}\tag{1.1.4a}
$$
где $min$ — это конечно же обозначение для минимума, то есть наименьшего из чисел.
Из $\eqref{eq:1.1.4}$ и $\eqref{eq:1.1.4a}$ вытекают следующие неравенства:
$$
\begin{matrix}
-|a| \leqslant \;\;\,a \leqslant |a| \\
-|a| \leqslant -a \leqslant |a|
\end{matrix} \label{eq:1.1.5}\tag{1.1.5}
$$
Заметим, что в каждом из двойных неравенств $\eqref{eq:1.1.5}$ как минимум одно из «внутренних» неравенств является равенством.
Для первого из них левое неравенство обращается в равенство при неположительном $a$, второе же обращается в равенство при неотрицательном $a$. Во втором двойном неравенстве из $\eqref{eq:1.1.5}$ всё наоборот. В частности при $а=0$ (и только в этом случае) все неравенства становятся равенствами.
Наконец, упомянем о квадратном корне, как об еще одной возможности записать абсолютную величину
одной формулой, а именно: $|a|=\sqrt{a^2}$ для любого вещественного числа. Однако это трудно принять в качестве определения абсолютной величины, скорее это следствие из определения арифметического квадратного корня, как неотрицательного числа, квадрат которого равен заданному. Впрочем, подобное равенство можно записать для любой четной степени:
$$
a = \sqrt[2n]{a^{2n}}, \qquad n=1, 2 ... \label{eq:1.1.6}\tag{1.1.6}
$$
Еще одно замечание на эту тему:
$$
|a|^{2n} = a^{2n}, \qquad n=1, 2 ... \label{eq:1.1.7}\tag{1.1.7}
$$
Другими словами: при взведении в четную степень знак абсолютной величины можно отбросить.
Можно также выразить абсолютную величину одной формулой, спрятав перебор возможных случаев в другую функцию.😉
Для этого прекрасно подходит функция «сигнум» (от латинского signum - знак), определяемая следующим образом:
$$
sgn(x) = \begin{cases}
\;\;\,1, \quad \text{если} \quad x \gt 0, \\
\;\;\,0, \quad \text{если} \quad x = 0, \\
-1, \quad \text{если} \quad x \lt 0
\end{cases} \label{eq:1.1.8}\tag{1.1.8}
$$
С помощью этой функции (введенной в XIX веке немецким математиком Леопольдом Кронекером (Leopold Kronecker)), абсолютную
величину можно записать в виде:
$$
|a| = a \; sgn(a) \label{eq:1.1.9}\tag{1.1.9}
$$
1.2. Интерпретация абсолютной величины на числовой оси. Простейшие уравнения и неравенства, содержащие абсолютную величину.
Легко видеть, что на числовой оси абсолютная величина числа — это расстояние от соответствующей точки до нулевой точки.
Заметим, что расстояние не может быть отрицательным, что дает другое подтверждение неравенству $\eqref{eq:1.1.2}$.
Применение абсолютной величины к неотрицательному числу оставляет соответствующую точку на месте, для отрицательных чисел точка заменяется симметричной ей точкой относительно нуля.
Обратимся к уравнению $|x|=a$, которое можно интерпретировать следующим образом: найти на числовой оси точки,
расстояние от которых до нуля равно $a$.
Понятно, что при $a \lt 0$ ставить вопрос бессмысленно, поэтому таких чисел не существует. При $a>0$ существует две точки, удаленные от нулевой на расстоянии $a$, соответствующие числам $x_1=a$ и $x_2=-a$. Для краткости эти решения можно записать одним равенством, используя знак $\pm$:
$$
|x| = a \; \Leftrightarrow \; x = \pm a \quad (a \gt 0) \label{eq:1.2.1}\tag{1.2.1}
$$
где знак $\Leftrightarrow$ означает «тогда и только тогда».
При $a=0$ решения сливаются в одно. В этом случае говорят, что уравнение имеет единственное решение: $x=0$.
$$
|x| = 0 \; \Leftrightarrow \; x = 0 \label{eq:1.2.2}\tag{1.2.2}
$$
Теперь рассмотрим неравенство $|x| \leqslant a$. В этом случае на числовой оси следует найти точки, расстояние от которых до нуля
не превосходит $a$
Снова $a$ не может быть отрицательным, так как в этом случае расстояние от точки до нуля было бы также отрицательным.
При $a \gt 0$ множество точек, расстояние от которых до нуля не меньше $a$ является отрезком, концы которого соответствуют числам
$-a$ и $a$:

Такое множество соответствует числовому отрезку $[-a, a]$, Таким образом:
$$
|x| \leqslant a \; \Leftrightarrow \; x \in [-a, a] \quad (a \gt 0) \label{eq:1.2.3}\tag{1.2.3}
$$
или
$$
|x| \leqslant a \; \Leftrightarrow \; -a \leqslant x \leqslant a \quad (a \gt 0) \label{eq:1.2.3a}\tag{1.2.3a}
$$
При $a=0$ получаем отрезок [0,0], содержащий лишь нулевую точку, поэтому:
$$
|x| \leqslant 0 \; \Leftrightarrow \; x=0 \label{eq:1.2.4}\tag{1.2.4}
$$
Если в исходное нестрогое неравенстве заменить строгим (получаем $|x| \lt a$), отрезок [-a, a] заменятся интервалом $(-a, a)$:
$$
|x| \lt a \; \Leftrightarrow \; x \in (-a, a) \quad (a \gt 0) \label{eq:1.2.5}\tag{1.2.5}
$$
или
$$
|x| \lt a \; \Leftrightarrow \; -a \lt x \lt a \quad (a \gt 0) \label{eq:1.2.5a}\tag{1.2.5a}
$$
Так как интервал $(0, 0)$ не содержит точек, неравенство имеет решение лишь при положительном $a$:
Наконец, перейдем к неравенству $|x| \geqslant a$.
Из $\eqref{eq:1.1.2}$ следует, что неравенству $|x| \geqslant 0$ удовлетворяет любое вещественное число. Более того, поскольку нуль больше любого отрицательного числа, неравенство $|x| \geqslant a$ заведомо верно для отрицательного $a$. Другими словами, при $a \leqslant 0$ решением неравенства $|x| \geqslant a$ является все множество действительных чисел: $x \in (-\infty, +\infty)$.
В случае положительного $a$ следует найти множество точек числовой оси, расстояние от которых до нулевой точки не меньше $a$.

Из приведенного чертежа видно, что такое множество разбивается на два полуинтервала, соответствующих положительным и отрицательным значениям $x$. Таким образом решением неравенства является объединение полуинтервалов $(-\infty, -a]$ и $[a, +\infty)$:
$$
|x| \geqslant a \; \Leftrightarrow \; x \in (-\infty,-a]\,\cup\, [a,+\infty) \quad (a \gt 0) \label{eq:1.2.6}\tag{1.2.6}
$$
а также
$$
|x| \geqslant a \; \Leftrightarrow \; x \leqslant -a \; \text{или} \; x \geqslant a \quad (a \gt 0) \label{eq:1.2.6a}\tag{1.2.6a}
$$
В случае строгого неравенства $|x| \gt a$ полуинтервалы заменяются интервалами:
$$
|x| \gt a \; \Leftrightarrow \; x \in (-\infty,-a)\,\cup\, (a,+\infty) \quad (a \gt 0) \label{eq:1.2.7}\tag{1.2.7}
$$
$$
|x| \gt a \; \Leftrightarrow \; x \lt -a \; \text{или} \; x \gt a \quad (a \gt 0) \label{eq:1.2.7a}\tag{1.2.7a}
$$
Следует заметить, что в случае отрицательного $a$ неравенству $|x| \gt a$ по-прежнему удовлетворяют все действительные числа,
в то время как неравенству $|x| \gt 0$ удовлетворяют все числа, кроме нуля:
$$
|x| \gt 0 \; \Leftrightarrow \; x \in (-\infty, 0)\,\cup\, (0, +\infty) \quad \label{eq:1.2.8}\tag{1.2.8}
$$
$$
|x| \gt 0 \; \Leftrightarrow \; x \ne 0 \label{eq:1.2.8a}\tag{1.2.8a}
$$
1.3. Арифметические операции над абсолютными величинами.
Примечательным свойством абсолютной величины является следующее:
Утверждение 1.3.1. Абсолютная величина произведения равна произведению абсолютных величин:
$$
|ab| = |a| \cdot |b| \label{eq:1.3.1}\tag{1.3.1}\
$$
Доказательство. Сказать: «это очевидно» — значит вызвать недовольство читателей, тем более, что многие факты предыдущих глав «за очевидностью» оставлены без доказательства, рассмотреть все возможные случаи — скучно и тоскливо. Мы выберем нечто среднее, прибегнув к квадратному корню. Итак:
$$
|ab| = \sqrt{(ab)^2} = \sqrt{a^2 b^2} = \sqrt{a^2} \cdot \sqrt{b^2} = |a| \cdot |b|
$$
Утверждение 1.3.1a. Абсолютная величина частного равна частному абсолютных величин:
$$
\left|\frac{a}{b}\right| = \frac{|a|}{|b|} \quad (b \ne 0) \label{eq:1.3.1a}\tag{1.3.1a}\
$$
В качестве доказательства достаточно применить утверждение 1.3.1 к числам $\dfrac{a}{b}$ и $b$.
Жить было бы намного легче, если бы аналогичные утверждения имели место для абсолютной величины суммы и разности. Оказывается в общем случае это неверно, однако некоторые утешительные факты все же имеются, коим посвящена эта глава.
Утверждение 1.3.2 (неравенство треугольника). Абсолютная величина суммы не превосходит суммы абсолютных величин:
$$
|a+b| \leqslant |a| + |b| \label{eq:1.3.2}\tag{1.3.2}
$$
причем равенство имеет место тогда и только тогда, когда хотя бы одно из слагаемых равно нулю, или слагаемые одинакового знака.
Доказательство.
Из неравенства $\eqref{eq:1.1.5}$ следует:
$$
\begin{array}{r}
-|a| \leqslant a \leqslant |a| \\
-|b| \leqslant b \leqslant |b|
\end{array}
$$
Складывая эти неравенства получаем:
$$
-(|a|+|b|) \leqslant a+b \leqslant |a|+|b| \label{eq:1.3.3}\tag{1.3.3}
$$
Число $|a|+|b|$ заведомо неотрицательно, что позволяет применить $\eqref{eq:1.2.3a}$. Получаем: $|a+b| \leqslant |a|+|b|$, что в точности совпадает с $\eqref{eq:1.3.2}$.
Проследим, в каких случаях неравенство $\eqref{eq:1.3.2}$ становится равенством. Для этого необходимо и достаточно, чтобы хотя бы одно из неравенств двойного неравенства $\eqref{eq:1.3.3}$ обратилось в равенство.
Так как левое неравенство $-(|a|+|b|) \leqslant a+b$ получено сложением неравенств $-|a| \leqslant a$ и $-|b| \leqslant b$,
оба этих неравенства должны быть равенствами: $|a|=-a, \; |b|=-b$. Это имеет место тогда и только тогда, когда $a$ и $b$ оба неположительны. Аналогично неравенство $a+b \leqslant |a|+|b|$ обращается в равенство тогда и только тогда, когда $a$ и $b$ оба неотрицательны. Таким образом числа $a$ и $b$ должны иметь одинаковые знаки, или хотя бы одно из них должно быть нулем, что завершает доказательство.
С помощью метода математической индукции неравенство $\eqref{eq:1.3.2}$ можно распространить на произвольное количество слагаемых:
$$
|a_1+a_2 + ... + a_n| \leqslant |a_1| + |a_2| + ... + |a_n| \label{eq:1.3.4}\tag{1.3.4}
$$
причем равенство имеет место тогда и только тогда, когда все слагаемые, за исключением возможных нулей, имеют одинаковые знаки.
Утверждение 1.3.3 (второе неравенство треугольника). Абсолютная величина разности не меньше разности абсолютных величин:
$$
|a-b| \geqslant ||a|-|b|| \label{eq:1.3.5}\tag{1.3.5}
$$
причем равенство имеет место тогда и только тогда, когда хотя бы одно из слагаемых равно нулю, или слагаемые одинакового знака.
Доказательство.
Рассмотрим два случая
А) $|a| \geqslant |b|$. Применяя неравенство треугольника $\eqref{eq:1.3.2}$ к числам $(a-b)$ и $b$, получаем:
$$
|(a-b)+b| \leqslant |a-b| + |b|
$$
Раскроем скобки, перенесем слагаемое $|b|$ влево и прочтем в обратную сторону. Получим:
$$
|a-b| \geqslant |a| - |b|
$$
Так как по предположению $|a| \geqslant |b|$, правая часть неотрицательна и ее можно заменить на $||a|-|b||$, что приводит к доказываемому неравенству $\eqref{eq:1.3.5}$
Осталась «самая малость»: разобраться, когда неравенство обращается в равенство. Согласно утверждению 1.3.2, это происходит
тогда и только тогда, когда либо числа $(a-b)$ и $b$ одинакового знака либо одно из них равно нулю. Докажем, что это эквивалентно
тому, что числа $а$ и $b$ одинакового знака, или одно из них равно нулю.
Если $b=0$, то всё в порядке, если $a-b=0$, то $a=b$, следовательно $a$ и $b$ — оба нули или одинакового знака, так что тоже все в порядке.
Пусть числа $(a-b)$ и $b$ одинакового знака. Если они оба положительны, то $a>b>0$, поэтому числа $a$ и $b$ оба положительны. Если $(a-b)$ и $b$ оба отрицательны, то $a \lt b \lt 0$, так что числа $a$ и $b$ оба отрицательны.
Теперь рассмотрим случай, когда числа $(a-b)$ и $b$ разных знаков. Если $b \lt 0$, то $(a-b)$ положительно, то есть $a \gt b$. При этом если $a$ неположительно, то из $b \lt a \leqslant 0$ следует $|a| \lt |b|$, тогда как по предположению $|a| \geqslant |b|$. Таким образом $a$ — положительно, следовательно числа $a$ и $b$ разных знаков. Случай $b \gt 0$ рассматривается аналогично.
Итак, доказательство ... нет, не завершено. Осталось рассмотреть еще одну возможность.
Б) $|a| \lt |b|$. В таком случае $|b| \gt |a|$, а это покрывается случаем А! Получаем:
$$
|b-a| \geqslant ||b|-|a||
$$
причем равенство имеет место тогда и только тогда ... (продолжите сами). Осталось лишь заметить, что, согласно $\eqref{eq:1.1.3}$, $|b-a| = |a-b|$ и $||b|-|a||=||a|-|b||$. Теперь доказательство действительно завершено.
Если в неравенствах $\eqref{eq:1.3.2}$ и $\eqref{eq:1.3.5}$ заменить $b$ на $-b$, то ввиду четности абсолютной величины (равенство $\eqref{eq:1.1.3}$) получим неравенства:
$$
\begin{array}{r}
|a-b| \leqslant |a| + |b|\\
|a+b| \geqslant ||a| - |b||\\
\end{array}
$$
которые можно объединить с исходными неравенствами, используя знак $\pm$:
$$
\begin{array}{r}
|a \pm b| \leqslant |a| + |b|\\
|a \pm b| \geqslant ||a| - |b||\\
\end{array}
$$
В свою очередь, полученные неравенства можно записать в виде двойного неравенства:
$$
||a| - |b|| \leqslant |a \pm b| \leqslant |a| + |b| \label{eq:1.3.6}\tag{1.3.6}
$$
которое в частности содержит в себе оба неравенства треугольника.
На самом деле, утверждения 1.3.2 и 1.3.3 допускают следующее уточнение:
Утверждение 1.3.4. Пусть вещественные числа $a$ и $b$ отличны от нуля. Если эти числа одинакового знака, то
$$
\begin{array}{c}
|a + b| = |a| + |b| \\
|a - b| = ||a| - |b|| \\
\end{array} \label{eq:1.3.7}\tag{1.3.7}
$$
при различных знаках:
$$
\begin{array}{c}
|a + b| = ||a| - |b|| \\
|a - b| = |a| + |b| \\
\end{array} \label{eq:1.3.8}\tag{1.3.8}
$$
Доказательство. Случай одинаковых знаков рассмотрен ранее. Если числа $a$ и $b$ имеет различные знаки, то знаки чисел $a$ и $(-b)$ совпадают,
поэтому к ним применимы неравенства $\eqref{eq:1.3.7}$. Получаем:
$$
\begin{array}{c}
|a + (-b)| = |a| + |b| \\
|a - (-b)| = ||a| - |b|| \\
\end{array}
$$
что после раскрытия скобок дает в точности $\eqref{eq:1.3.8}$.
Приведенный чертеж иллюстрирует полученное свойство. Видно, что в при одинаковы знаках сложение чисел приводит к сложению их абсолютных величин, а при вычитании чисел их абсолютные величины вычитаются. В случае разных знаков наоборот, сложение чисел приводит к вычитанию абсолютных величин, а при вычитании чисел их абсолютные величины складываются.

В заключение заметим, что если хотя бы одно из чисел $a$ и $b$ равно нулю (и только в этом случае) все четыре неравенства из $\eqref{eq:1.3.7}$ и $\eqref{eq:1.3.8}$ обращаются в равенства.
1.4 Абсолютная величина, как функция.
Обратимся теперь к функции $y = |x|$. Из определения абсолютной величины $\eqref{eq:1.1.1a}$ следует, эта функция совпадает с функцией $y=x$ при неотрицательных $x$ и с функцией $y=-x$ при отрицательных $x$, что дает возможность построить ее график.

График функции симметричен относительно оси ординат, следовательно функция является четной, что согласуется с $\eqref{eq:1.1.3}$.
Важным свойством функции $y=|x|$ является ее непрерывность. Таким образом, из непрерывности функция $f(x)$ следует непрерывность ее абсолютной величины $|f(x)|$. Как будет указано в дальнейшем, это свойство можно использовать для
проверки правильности составления уравнений или неравенств при применении метода интервалов.
Как следует из построения графика, производная функции |x| равна 1 при положительном $x$, где функция |x| монотонно возрастает.
При отрицательном $x$ производная равна (-1), что соответствует убыванию функции. Таким образом, минимум функции, достигается при $x=0$
и равен нулю, что соответствует началу координат. Начало координат — единственная точка графика, лежащая на оси абсцисс, остальные точки лежат в верхней полуплоскости, в соответствии с неотрицательностью абсолютной величины. Другими экстремумами функция не обладает.
Заметим, что начало координат является точкой излома графика, так как в этой точке левая и правая производные не совпадают. Таким образом функция |x| является кусочно-дифференцируемой, областью определения ее производной является числовая ось с «выколотой» нулевой точкой: $(-\infty,0)\;\cup\;(+\infty, 0)$. В этой области производная совпадает с ранее упомянутой функцией
$sgn(x)$ (см. $\eqref{eq:1.1.8}$), и только в нуле функции отличаются. Поскольку единственная точка с конечным значением не влияет на интегрирование, функция $|x|$ является первообразной для $sgn(x)$:
$$
\int {sgn(x)\;dx} = |x| + C
$$
так что
$$
\int\limits_a^b {sgn(x)\;dx} = |b| - |a|
$$
Из непрерывности функции $|x|$ следует ее интегрируемость. Однако оставлю вычисление первообразной в качестве задачи.
Функция |x| является выпуклой (вниз), так как любой отрезок соединяющий точки ее графика лежит не ниже графика.
Для заданной функции $f(x)$ требуется построить графики функций $f(|x|)|$, $|f(x)|$ и $|f(|x|)|$
Будем считать, то график функции $f(x)$ уже построен и постараемся его превратить в график функции $f(|x|)$. При $x \geqslant 0$ знак абсолютной величины можно просто опустить, так что в этой случае значение функции не изменяется. Так как что множеством точек с $x \geqslant 0$ является правая полуплоскость, точки графика лежащие на оси ординат (Oy) и справа от нее остаются без изменений. Займемся точками слева от оси Oy. Если $x \lt 0$, то $f(|x|)=f(-x)$. Это значит, что значение ординаты каждой точки графика с $x \lt 0$ заменить ординатой точки графика с абсциссой $-x$. Так как точка с абсциссой $-x$ лежит в правой полуплоскости, часть графика, лежащая слева от оси ординат нас не интересует и ее можно аккуратно стереть, заменив зеркально отображенной правой полуплоскостью. Итак, для получения графика функции $f(|x|)$ из графика функции $f(x)$ следует заменить часть в лежащую в левой полуплоскости частью, лежащей в правой полуплоскости, зеркально отраженной относительно оси ординат. В связи с этим функция $f(|x|)$ – заведомо четная, независимо от поведения $f(x)$.
Теперь обратимся к графику функции $|f(x)|$. В этом случае нас будет интересовать не знак аргумента, а знак функции. При неотрицательных значениях $f(x)$ (соответствующие точки графика лежат в верхней полуплоскости, включая ось абсцисс) значения функций $f(x)$ и $|f(x)|$ совпадают. Если $f(x) \lt 0$ (соответствующая точка графика лежит ниже оси абсцисс), то $|f(x)|$ противоположна $f(x)$. Замечая, что точки $(x, f(x))$ и $(x, -f(x))$ симметричны друг другу относительно оси абсцисс (Ox), приходим следующему выводу: для получения графика функции $|f(x)|$ из графика функции $f(x)$ следует часть графика, лежащую в нижней полуплоскости, заменить ее зеркальным отображением относительно оси абсцисс. Важно заметить, что в отличие от предыдущего случая, происходит не замещение, а объединение отраженной части с уже существующей частью графика, тогда как нижняя полуплоскость (вне оси Ox) очищается от точек графика.
Наконец, для построения графика функции $|f(|x|)|$ выполняем обе операции: сначала заменяем левую часть графика отраженной правой, затем отражаем его нижнюю часть вверх. (Можно и в обратном порядке.)
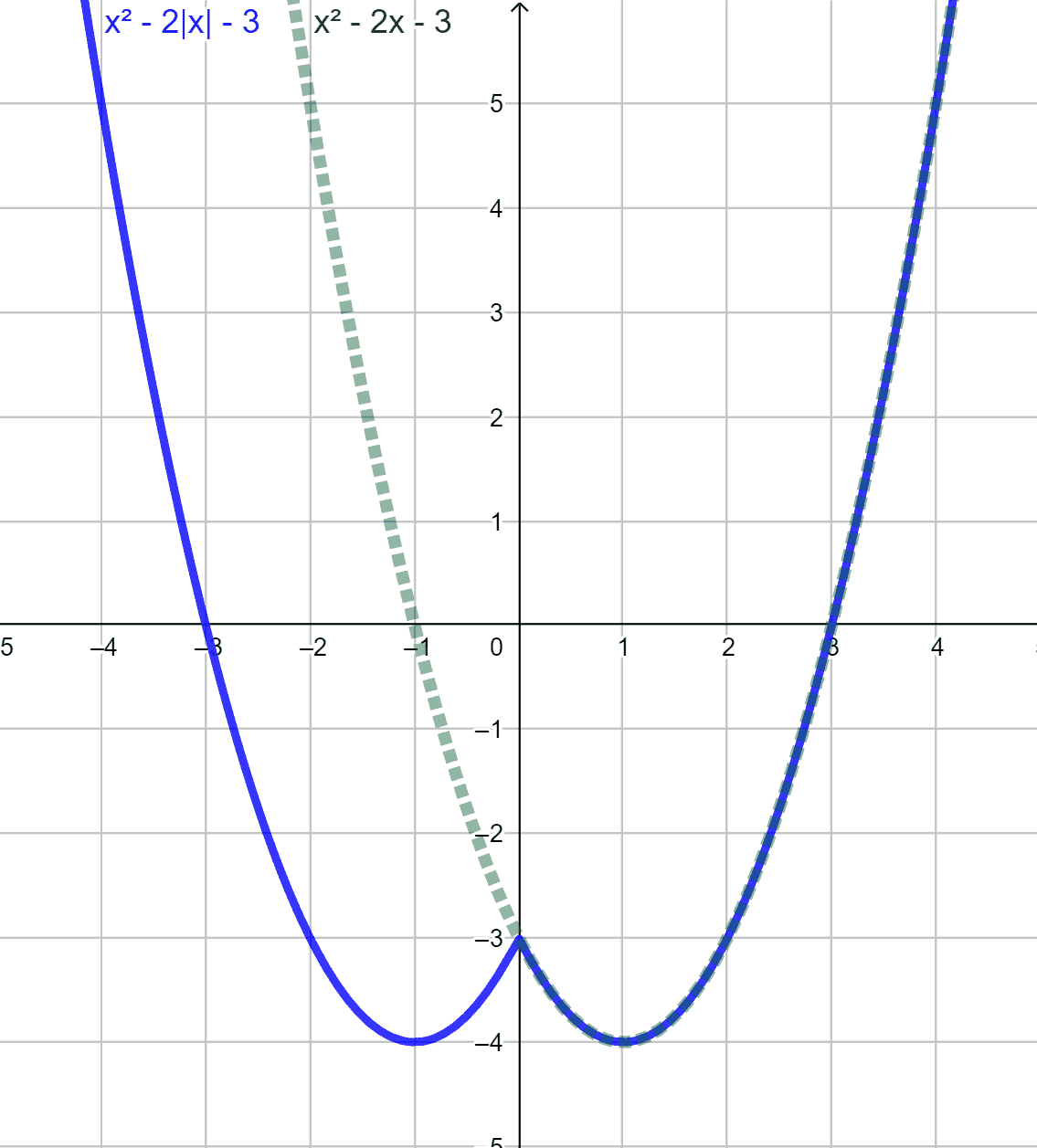
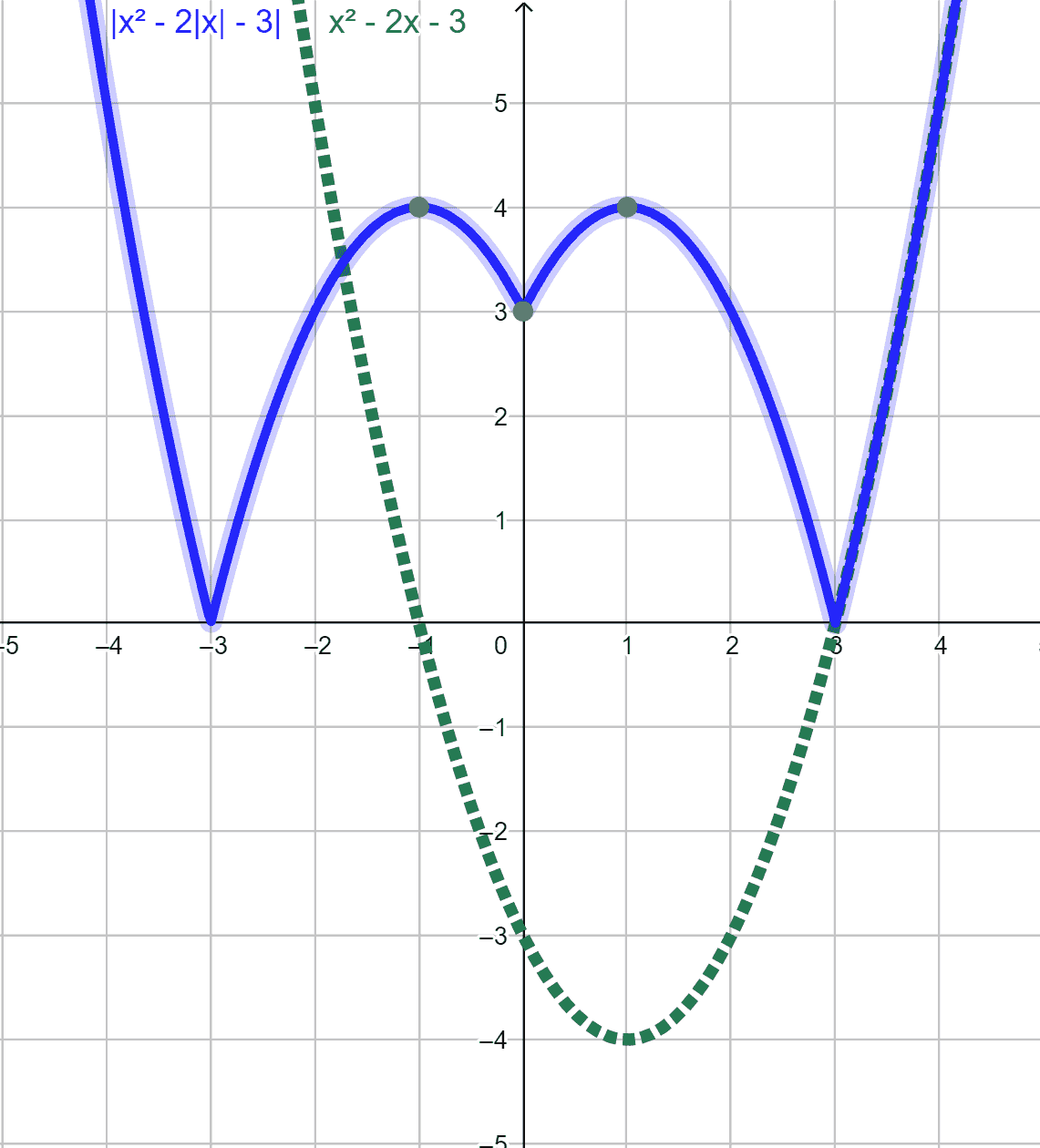
На чертеже изображено получение графика функций $x^2-2|x|-3$, $|x^2-2x-3|$ и $|x^2-2|x|-3|$ (синие) из графика функции $x^2-2x-3$ (зеленый).
2 Распространение абсолютной величины на комплексные числа.
2.1. О комплексных числах.
Для тех, кто незнаком, или позабыл о том, что такое комплексное числа, замечу, что таковым является число вида
$$
z = a + bi \label{eq:2.1.1}\tag{2.1.1}
$$
где $i$ – так называемая мнимая единица (от латинского imaginarium — мнимый, воображаемый), одно из чисел, квадрат которого равен (-1) Другим таким числом является конечно же $(-i)$. (Но ведь нас в школе учили, что квадратный корень из отрицательных чисел не существует! В действительности это так, однако от воображаемых чисел всё можно ожидать!). Числа $a$ и $b$ называются соответственно действительной и мнимой частью комплексного числа $z$. Число вида $a+0i$ с нулевой мнимой частью отождествляются с действительным (вещественным) числом $a$. Напротив, число вида $0+bi$ при $b \ne 0$ записывается, как $bi$, и называется чисто мнимым, таковыми в частности являются числа $i$ и $-i$.
При сложении и вычитании комплексных чисел их действительные и мнимые части складываются и вычитаются в отдельности:
$$
(a + bi) \pm (c+di) = (a \pm c) + (b \pm d)i \label{eq:2.1.2}\tag{2.1.2}
$$
Комплексные числа можно перемножить обычным раскрытием скобок, заменив $i^2$ на (-1):
$$
(a + bi) (c+di) = ac + bci + adi + bdi^2 = ac + bci + adi - bd = (ac-bd) + (bc+ad)i \label{eq:2.1.3}\tag{2.1.3}
$$
В частности, при $d=0$ получаем:
$$
(a + bi) \cdot c = ac + bci\,, \label{eq:2.1.4}\tag{2.1.4}
$$
то есть при умножении на вещественное число достаточно каждую часть умножить на это число. При умножении на (-1) можно просто поставить знак «-» перед числом:
$$
-z = -(a+bi) = -a - bi \label{eq:2.1.5}\tag{2.1.5}
$$
При делении комплексных чисел (при этом делитель, конечно, должен быть отличен от нуля) следует делимое и делитель умножить на число, комплексно-сопряженное делителю (знак мнимой части меняется на противоположный):
$$
\frac{a+bi}{c+di} = \frac{(a+bi)(c-di)} {(c+di)(c-di)} = \frac{(ac+bd)+(bc-ad)i}{c^2+d^2} = \frac{ac+bd}{c^2+d^2} + \frac{bc-ad}{c^2+d^2}\;i \label{eq:2.1.6}\tag{2.1.6}
$$
(Заметим, что так как делитель $c+di$ отличен от нуля, одно из чисел $c$ и $d$ отлично от нуля, поэтому $c^2+d^2>0$, что гарантирует существование результата.)
Из вышесказанного следует, что множество комплексных чисел замкнуто относительно арифметических операций. Кроме того, как утверждает основная теорема алгебры, во множестве комплексных чисел всякий многочлен с комплексными коэффициентами и отличный от константы (т.е. $0x+b$) имеет корень, тогда как множество вещественных чисел не обладает аналогичным свойством.
Поскольку множество действительных чисел населяет всю числовую ось, для размещения комплексных чисел, требуется перейти во второе измерение. Таким образом, приходим к понятию комплексная плоскость, где вдоль оси абсцисс, называемой в данном случае действительной осью, располагаются вещественные числа, а вдоль оси ординат (мнимая ось) располагаются чисто-мнимые числа. Что же касается остальных, то в их распоряжении вся плоскость: комплексному числу $(a+bi)$ соответствует точка комплексной плоскости с координатами $(a, b)$.
Вспомнив, что абсолютная величина вещественного числа, есть расстояние от соответствующей точки числовой оси до нулевой точки, можно распространить это понятие на комплексные числа, рассматривая расстояние от соответствующей точки комплексной плоскости до начала координат. Такая величина называется модулем комплексного числа и служит обобщением понятия «абсолютная величина» для комплексных чисел. Так же, как и для абсолютной величины, для обозначения модуля используются вертикальные черточки |...|.
Как следует из теоремы Пифагора,
$$
|a+bi| = \sqrt{a^2+b^2}, \label{} \label{eq:2.1.7}\tag{2.1.7}
$$
откуда, в частности, учитывая $\ref{eq:2.1.5}$, получаем:
$$
|-z| = |z| \label{eq:2.1.8}\tag{2.1.8}
$$
Проведем вектор из начала координат в точку, соответствующую комплексному числу. Такой вектор будем называть радиус-вектором, соответствующим данному комплексному числу:

Длина вектора (называемая нормой или модулем вектора), которая обычно обозначается буквой $r$, равна модулю комплексного числа, а угол $\varphi$ между вектором и положительным направлением действительной оси, называемый аргументом комплексного числа определяется из равенств:
$$
\begin{array}{c}
cos\;\varphi = \dfrac{a}{r} = \dfrac{a}{\sqrt{a^2+b^2}},\\
sin\;\varphi = \dfrac{b}{r} = \dfrac{b}{\sqrt{a^2+b^2}}
\end{array} \label{eq:2.1.9}\tag{2.1.9}
$$
Знакомые с полярной системой координат наверное уже заметили, что $(r, \varphi)$ являются полярными координатами точки комплексной плоскости,
если, как обычно, считать полюсом начало координат, а полярной осью положительное направление оси абсцисс (т.е. действительной оси).
Из $\eqref{eq:2.1.9}$ следует:
$$
a = r \cdot cos\; \varphi, \quad b = r \cdot sin\;\varphi \label{eq:2.1.10}\tag{2.1.10}
$$
что позволяет переписать равенство $\eqref{eq:2.1.1}$ в виде:
$$
z = r(cos\;\varphi + i\;sin\;\varphi) \label{eq:2.1.11}\tag{2.1.11}
$$
Такая запись называется тригонометрической формой комплексного числа. Важно заметить, что если комплексное число $z$ удалось выразить в виде $\eqref{eq:2.1.11}$, то $r$ обязано быть его модулем, хотя бы потому что, применяя $\eqref{eq:2.1.7}$ к равенству $\eqref{eq:2.1.11}$, получаем:
$$
|z| = \sqrt{(r \; cos\; \varphi)^2 + (r \; sin\; \varphi)^2} = \sqrt{r^2 cos^2 \varphi + r^2 sin^2 \varphi} = \sqrt{r^2} = r
$$
Что же касается аргумента, то ввиду периодичности синуса и косинуса, его значение из $\eqref{eq:2.1.9}$ определяется неоднозначно. Можно потребовать, чтобы аргумент всегда находится в промежутке $[0, 2\pi)$, однако на практике это приводит к некоторой «неловкости». Проще всего договориться, что если аргументы отличаются на число, кратное $2\pi$, они считаются равными. В случае $a=b=0$ (т.е. при $z=0$) каждая из формул $\eqref{eq:2.1.9}$ дает неопределенность вида $\frac{0}{0}$, поэтому аргументом нуля может служить любое число.
Для знакомых с мнимым показателем степенями замечу, что тригонометрическую форму можно записать короче, как $z=re^{\varphi i}$,
что значительно упрощает многие выкладки, однако воздержусь от такого соблазна, дабы не искушать непосвященных читателей.
2.2. Взглянем по-новому!
Переход в новое измерение позволяет увидеть полную картину того, что мы наблюдали раньше.
Формула $|a|=\sqrt{a^2}$ для действительного числа является всего лишь частным случаем $\eqref{eq:2.1.7}$ при $b=0$. Зато
точный аналог тождества $|a|^{2k} = a^{2k}$ не применим к комплексным числам, так как при $a$ и $b$ отличных от нуля степень $a+bi$
не является даже вещественным числом. Однако равенство можно слегка подправить, чтобы оно стало верным:
$|z^n| = |z|^n$, при этом $n$ может быть любым натуральным числом (доказательство далее в главе 2.3).
Взглянем по-новому на уравнение $|x| = a$, которое, в применении к комплексным числам уместнее записать в виде $|z| = r$.
Как и в случае вещественных чисел, решение существует тогда и только тогда, когда правая часть неотрицательна, однако при $r \gt 0$ уравнение вместо двух точек дает окружность радиуса $r$ с центром в начале координат, и только при $r=0$ получаем всё тот же единственный и неповторимый нуль.
Решением неравенства $|z| \leqslant r$ при $r \gt 0$ является множество точек круга радиуса $r$ включая точки окружности,
а при $r=0$ это множество сжимается в начало координат, то есть нуль. В случае строгого неравенства $|z| \lt r$ точки окружности
следует исключить, что снова не оставляет решений при $r=0$.
Интересно подсчитать количество целочисленных решений уравнения $z \leqslant r$. (Целочисленным, как вы конечно догадались, будем называть решение, в котором действительная и мнимая части являются целыми числами.) В вещественном случае такие числа можно пересчитать «на пальцах»: $0$, $\pm 1$ ... $\pm \lfloor a \rfloor$, где $\lfloor \dots \rfloor$ используется для обозначения целой части числа (т.е. наибольшего целого числа, не превосходящего заданное). Таким образом, общее количество
целочисленных решений неравенства $|x| \leqslant a$ на множестве вещественных чисел равно $2\lfloor a \rfloor + 1$.
В применении к комплексным числа задачу можно переформулировать следующим образом:
в круге радиуса $r$ с центром в начале координат найти количество точек, обе координаты которых являются целыми числами;
или еще проще:
найти количество целочисленных решений неравенства $x^2 + y^2 \leqslant r^2$
Понятно, что в круг радиуса $r$ кроме действительных чисел $0$, $\pm 1$, $\pm 2$ ... $\pm \lfloor r \rfloor $, попадают также чисто-мнимые числа $\pm i$,
$\pm 2i$ ... $\pm \lfloor r \rfloor i$, что дает нижнюю оценку искомого числа, обозначаемого через $N(r)$:
$$
N(r) \geqslant 4 \lfloor r \rfloor + 1
$$
однако такая (весьма примитивная) оценка точна лишь для $r \lt \sqrt{2}$, с увеличением $r$ количество «дополнительных точек» значительно превышает количество осевых.
Можно исходить из формулы площади круга, полагая что каждая точка решетки 1 × 1 содержит в среднем по одной точке с целочисленными координатами. Таким образом
$$
N(r) \approx \lfloor \pi r^2 \rfloor
$$
Однако и такую оценку трудно назвать удовлетворительной. Круг радиуса 1 (или чуть больше 1) содержит 5 искомых точек, тогда как формула дает лишь 3, $N(\sqrt{2}) = 9$, тогда как по формуле выходит $\lfloor 2 \pi \rfloor = 6$.
Первый существенный прорыв на эту тему сделан «королем математики» Карлом Фридрихом Гауссом (Carl Friedrich Gauß), который нашел верхнюю оценку числа $N(r)$:
$$
N(r) \leqslant \pi r^2 + 2\sqrt{2} \pi r
$$
вследствие чего задача получила название «Проблема (задача) круга Гаусса» (англ. Gauss circle problem).
Точное значение $N(r)$ выражается бесконечной суммой:
$$
N(r)=1+4\sum_{i=0}^\infty \left(\left\lfloor\frac{r^2}{4i+1}\right\rfloor-\left\lfloor\frac{r^2}{4i+3}\right\rfloor\right)
$$
При составлении компьютерных программ по-видимому удобнее всего пользоваться формулой:
$$
N(r) = \sum\limits_{n=0}^{r^2}{r_2(n)} = r_2(0) + r_2(1) + ... + r_2(r^2)
$$
где $r_2(n)$ — количество представлений числа $n$ в виде суммы двух квадратов, причем пары, отличающиеся порядком и/или знаком считаются различными.
Например, $r_2(1)=4$, так как $1 = 0^2 + 1^2 = 0 + (-1)^2 = 1^2 + 0^2 = (-1)^2 + 0^2$, давая таким образом 4 различные пары.
2.3. Арифметические операции над модулями комплексных чисел.
Вернемся к главе 1.3 и попытаемся распространить содержащиеся там утверждения на комплексные числа.
Утверждение 2.3.1. Модуль произведения комплексных чисел равен произведению их модулей:
$$
|z_1\,z_2| = |z_1| \cdot |z_2| \label{eq:2.3.1}\tag{2.3.1}
$$
Доказательство.Проще всего это сделать, используя тригонометрическую форму. Напишем:
$$
\begin{array}{l}
z_1 = r_1\;(cos\;\varphi + i\; sin\;\varphi) \\
z_2 = r_2\;(cos\;\psi + i\; sin\;\psi) \\
\end{array}
$$
и будем перемножать не суетясь раскрывая скобки:
$$
\begin{align}
z_1z_2 & = r_1r_2\;(cos\,\varphi\;cos\,\psi+i\;cos\,\varphi\;sin\,\psi+i\;sin\,\varphi\;cos\,\psi+i^2\;sin\,\varphi\;sin\,\psi) \\
& = r_1r_2\;[(cos\,\varphi\;cos\,\psi-sin\,\varphi\;sin\,\psi)+i\;(sin\,\varphi\;cos\,\psi+cos\,\varphi\;sin\,\psi)]
\end{align}
$$
Однако выражения в круглых скобках нам хорошо знакомы! Хотите напомню? — Надеюсь, в этом нет необходимости.
Выражение в первой скобке — это не что иное, как косинус суммы, во второй скобке, конечно же, синус суммы. Итак, получаем:
$$
z_1z_2 = r_1r_2\;[cos(\varphi+\psi)+i\;sin(\varphi+\psi)] \label{eq:2.3.2}\tag{2.3.2}
$$
Стоит лишь сделать подстановку $\xi = \varphi + \psi$, как правая часть $\eqref{eq:2.3.2}$ принимает привычный вид:
$$
z_1z_2 = r_1r_2\;(cos\,\xi + i\,sin\,\xi)
$$
поэтому, как было замечено в конце главы 2.1, число $r_1r_2$, оно же $|z_1|\cdot|z_2|$, обязано быть модулем числа в левой части равенства, то есть
$|z_1z_2| = |z_1|\cdot|z_2|$, что и требовалось доказать.
На самом деле мы доказали даже большее: при перемножении комплексных чисел их модули перемножаются, а аргументы складываются. С помощью метода математической индукции результат можно распространить на произвольное количество сомножителей. В частности, когда все сомножители равны между
собой, получаем знаменитую формулу Муавра (Abraham de Moivre):
$$
z^n = [r(cos\,\varphi + i\,sin\,\varphi)]^n = r^n(cos\,n\varphi + i\,sin\,n\varphi) \label{eq:2.3.3}\tag{2.3.3}
$$
откуда следует ранее упомянутое тождество:
$$
|z^n| = |z|^n \label{eq:2.3.3a}\tag{2.3.3a}
$$
Утверждение 2.3.1а. Модуль частного комплексных чисел равен частному их модулей:
Доказательство.Пусть $z_2 \ne 0$ и $z_q = \dfrac{z_1}{z_2}$. Запишем:
$$
\begin{array}{l}
z_1 = r_1\;(cos\;\varphi + i\; sin\;\varphi) \\
z_2 = r_2\;(cos\;\psi + i\; sin\;\psi) \\
z_q = r_q\;(cos\;\xi + i\; sin\;\xi)
\end{array}
$$
Так как $z_1 = z_2\,z_q$, то, согласно равенству $\eqref{eq:2.3.2}$, имеем:
$$
\begin{array}{l}
r_1 = r_2 \cdot r_q \\
\varphi = \psi + \xi \quad \text{(«с точностью до }2\pi\text{»)}
\end{array}
$$
или
$$
|z_q| = r_q = \frac{r_1}{r_2}, \qquad \xi = \varphi - \psi
$$
Таким образом:
$$
\left|\frac{z_1}{z_2}\right| = \frac{r_1}{r_2}\,[cos(\varphi-\psi)+i\,sin(\varphi-\psi)]
$$
Другими словами: при делении комплексных чисел их модули делятся, а аргументы вычитаются.
Обратимся теперь к менее очевидным свойствам, относящимся к модулям суммы и разности. Сначала докажем их непосредственно, а затем посмотрим на это под другим углом.
Утверждение 2.3.2 (неравенство треугольника). Модуль суммы комплексных чисел не превосходит сумму модулей этих чисел.:
$$
|z_1 + z_2| \leqslant |z_1| + |z_2| \label{eq:2.3.4}\tag{2.3.4}
$$
причем равенство имеет место тогда и только тогда, когда хотя бы одно из слагаемых равно нулю, или аргументы слагаемых совпадают.
Доказательство. Запишем числа в тригонометрической форме:
$$
\begin{array}{l}
z_1 = r_1\;(cos\;\varphi + i\; sin\;\varphi) \\
z_2 = r_2\;(cos\;\psi + i\; sin\;\psi)
\end{array} \label{eq:2.3.5}\tag{2.3.5}
$$
Определим сумму чисел
$$
z_1 + z_2 = (r_1\,cos\,\varphi + r_2\,cos\,\psi) + i\,(r_1\,sin\,\varphi + r_2\,sin\,\psi)
$$
и вычислим ее модуль:
$$
\begin{align}
|z_1+z_2|^2 & = (r_1\,cos\,\varphi + r_2\,cos\,\psi)^2 + (r_1\,sin\,\varphi + r_2\,sin\,\psi)^2 \\
& = r_1^2 cos^2\varphi + 2r_1 r_2\, cos\,\varphi\;cos\,\psi + r_2^2cos^2\psi + r_1^2 sin^2\varphi + 2r_1 r_2\, sin\,\varphi\;sin\,\psi + r_2^2\,sin^2\psi\\
& = r_1^2(cos^2\varphi+sin^2\varphi) + 2r_1r_2(cos\,\varphi\;cos\,\psi+sin\,\varphi\;sin\,\psi) + r_2^2(cos^2\psi+sin^2\psi) \\
& = r_1^2 + 2r_1r_2cos(\varphi-\psi) + r_2^2 \label{eq:2.3.6}\tag{2.3.6}
\end{align}
$$
Учитывая, что $r_1$, $r_2$ — неотрицательны и $cos(\varphi-\psi) \leqslant 1$, получаем:
$$
|z_1+z_2|^2 = r_1^2 + 2r_1r_2cos(\varphi-\psi) + r_2^2 \leqslant r_1^2 + 2r_1r_2 + r_2^2 = (r_1 + r_2)^2 \label{eq:2.3.7}\tag{2.3.7}
$$
откуда (снова ввиду неотрицательности модулей)
$$
|z_1 + z_2| \leqslant r_1 + r_2
$$
или $|z_1 + z_2| \leqslant |z_1|+|z_2|$, qed.
Неравенство $\eqref{eq:2.3.7}$ (а следовательно и неравенство $\eqref{eq:2.3.4}$) обращается в равенство тогда и только тогда, когда
$$
2r_1r_2cos(\varphi-\psi) = 2r_1r_2
$$
или
$$
r_1r_2[cos(\varphi-\psi)-1] = 0
$$
В таком случае либо хотя один из модулей равен нулю, либо $cos(\varphi-\psi) = 1$, то есть $\varphi-\psi=2\pi k$, $k=0,\pm1,\pm2 \dots$, что, согласно нашему уговору, означает равенство аргументов.
И в этом случае неравенство треугольника распространяется на произвольное количество слагаемых:
$$
|z_1 + z_2 + \dots + z_n| \leqslant |z_1| + |z_2| + \dots + |z_n| \label{eq:2.3.8}\tag{2.3.8}
$$ причем равенство имеет место тогда и только тогда, когда все числа кроме возможных нулей имеют одинаковые аргументы.
Утверждение 2.3.3 (второе неравенство треугольника). Модуль разности комплексных чисел не меньше разности модулей этих чисел:
$$
|z_1 - z_2| \geqslant ||z_1| - |z_2|| \label{eq:2.3.9}\tag{2.3.9}
$$
причем равенство имеет место тогда и только тогда, когда хотя бы одно из слагаемых равно нулю, или аргументы слагаемых совпадают.
Заметим, что внешние черточки $|\dots|$ в правой части означают абсолютную величину, так как речь идет о вещественных числах.
Доказательство. В этот раз используем равенства \eqref{eq:2.3.5} для вычисления модуля разности:
$$
|z_1-z_2|^2 = r_1^2 - 2r_1r_2cos(\varphi-\psi) + r_2^2 \label{eq:2.3.10}\tag{2.3.10}
$$
Снова используем неотрицательность модулей и $cos(\varphi-\psi) \leqslant 1$, однако ввиду отрицательного знака перед $2r_1r_2\,cos(\varphi-\psi)$ знак неравенства будет направлен в другую сторону.
$$
|z_1-z_2|^2 \geqslant r_1^2 - 2r_1r_2 + r_2^2 = (r_1 - r_2)^2
$$
Теперь, поскольку выражение $(r_1 - r_2)$ может быть отрицательным, при извлечении квадратного корня появляется знак абсолютной величины:
$$
|z_1 - z_2| \geqslant |r_1 - r_2|
$$
или
$$
|z_1 - z_2| \geqslant ||z_1| - |z_2||
$$
Как и в предыдущем случае неравенство обращается в равенство при $r_1r_2[cos(\varphi-\psi)-1] = 0$, то есть при тех же условиях.
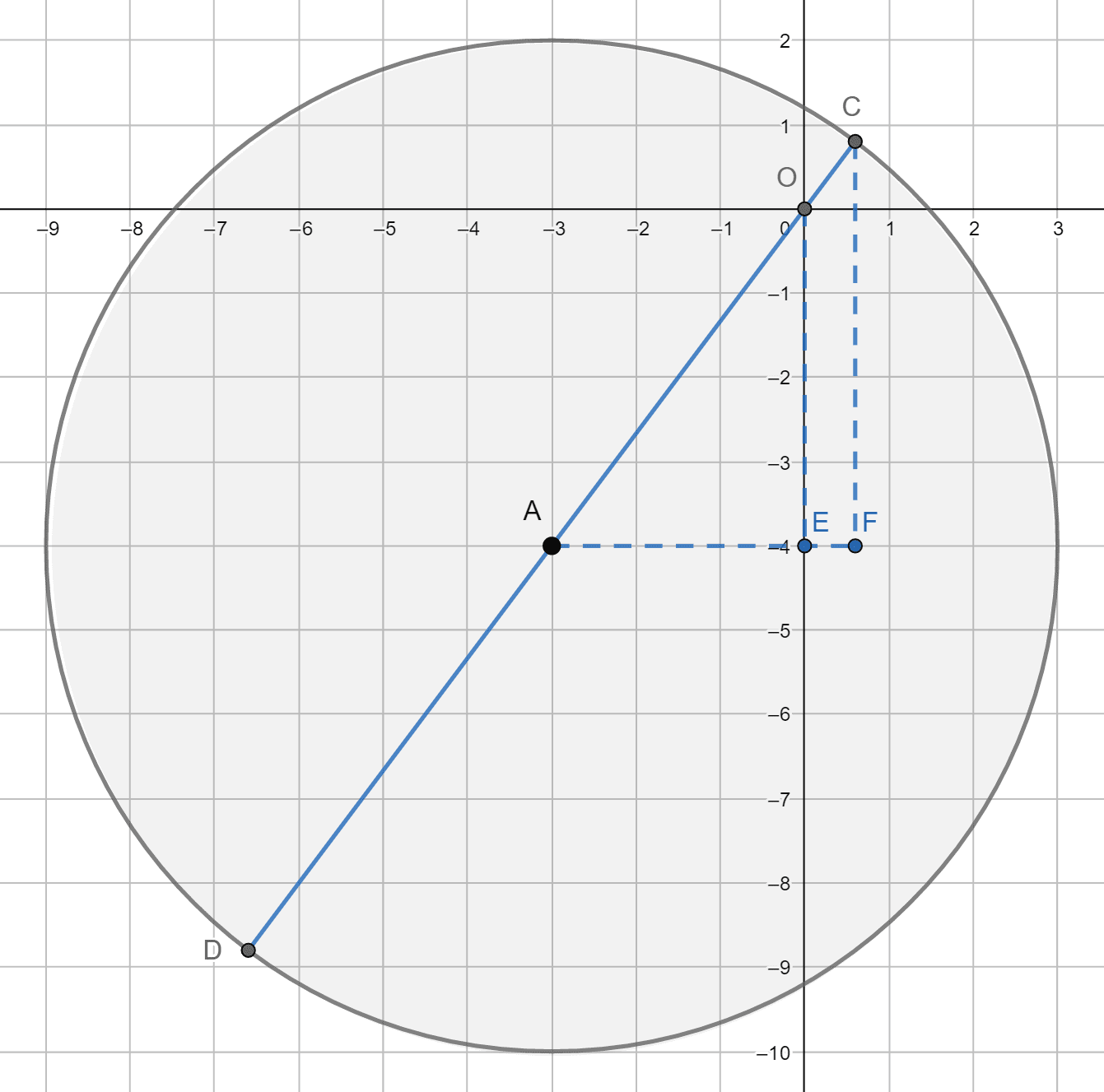
Для наглядной интерпретации полученных результатов, снова обратимся к радиус-векторам.
Можно заметить, что сложение и вычитание комплексных чисел равносильно сложению соответствующих радиус-векторов, а именно
радиус-вектор суммы/разности комплексных чисел является векторной суммой/разностью радиус-векторов этих чисел,
что иллюстрируется нижеследующим чертежом.

Заметим, что $\triangle OBC$, образован сторонами, длины которых равны $|z_1|$, $|z_2|$ и $|z_1+z_2|$. При этом даже совершенно далекие от математики знают, что в любом треугольнике длина стороны меньше суммы длин двух других сторон. Отсюда $|z_1 + z_2| \lt |z_1| + |z_2|$, что совпадает с $\eqref{eq:2.3.4}$ ... с точностью до строгости неравенства. Единственная возможность обратить неравенство в равенство — это превратить треугольник в вырожденный, расположив точки $O$, $B$ на $C$ одной прямой, кроме того, при этом точка $B$ должна располагаться между точками $O$ и $C$ или совпадать с одной из них, так как в противном случае модули не складываются, а вычитаются. В случае совпадения одно из чисел $|z_1|$, $|z_2|$ равно нулю, иначе векторы $\vec{OC}$ и $\vec{BC}$, соответствующие числам $z_1$ и $z_2$ являются коллинеарными и одинаково направленными, так что аргументы этих чисел равны.
Второе неравенство треугольника $\eqref{eq:2.3.9}$ является отсылкой к другому свойству стороны треугольника: длина стороны треугольника больше разности длин других сторон. $\triangle OAB$, длины сторон которого равны $|z_1|$, $|z_2|$ и $|z_1-z_2|$ иллюстрирует это свойство. Чтобы неравенство обратилось
в равенство необходимо, чтобы точки $О$ $A$ и $B$ располагались на одной прямой, а кроме того, либо одна из точек $A$ и $B$ совпала с $O$, либо обе точки находились по одну сторону от точки $O$. В последнем случае векторы $\vec{OA}$ и $\vec{OA}$ коллинеарны и одинаково направлены, следовательно их аргументы равны.
Попутно, из приведенного чертежа можно получить изящное тождество, вспомнив что сумма квадратов диагоналей прараллелограмма равна сумме квадратов его сторон. В применении к параллелограмму $OBCA$ это дает:
$$
|z_1 + z_2|^2 + |z_1 - z_2|^2 = 2|z_1|^2 + 2|z_2|^2 \label{eq:2.3.11}\tag{2.3.11}
$$
Тождество $\eqref{eq:2.3.11}$ называется тождеством (равенством) параллелограмма. Оно также вытекает из $\eqref{eq:2.3.6}$ и $\eqref{eq:2.3.10}$
Наконец, используя рассмотренную в главе 1.3 замену $z_2 = -z_2$, оба неравенства треугольника можно объединить:
$$
||z_1| - |z_2|| \leqslant |z_1 \pm z_2| \leqslant |z_1 + z_2| \label{eq:2.3.12}\tag{2.3.12}
$$
3. Абсолютная величина в уравнениях и неравенствах.
Трудно отказать себе в удовольствии привести некоторые примеры решения уравнений и неравенств с абсолютной величиной. Как было обещано в начале, попытаемся показать, что решение таких задач может действительно принести удовольствие.
3.1. Перебор промежутков нужен далеко не всегда!
Рассмотрим уравнение:
$$
|x^2-x-9| = 3 \label{eq:3.1.1}\tag{3.1.1}
$$
Кое-кто из консерваторов может настаивать на исследовании выражения под знаком абсолютной величины. Для этого приходится иметь дело с иррациональными корнями трехчлена $x^2-x-9$. Поднимите руки те, кому нравится работать с иррациональными числами. Не вижу рук! Конечно не всегда это можно избежать, но при возможности лучше держаться от иррациональностей подальше, так как работая с ними не мудрено совершить глупую ошибку.
Взглянем на уравнение $\eqref{eq:3.1.1}$ по-другому. Полагая $y=x^2-x-9$, приходим к уравнению $|y|=3$, решениями которого, как было указано в главе 1.2, являются $y=\pm 3$. Таким образом получаем:
$$
x^2-x-9 = \pm 3
$$
что дает два квадратных уравнения:
$$
\begin{align}
x^2-x-12 = 0\, & \Rightarrow\; x_1 = 4,\; x_2 = -3 \\
x^2-x-6 = 0 \, & \Rightarrow\; x_1 = 3, \; x_2 = -2
\end{align}
$$
Осталось лишь расположить корни в порядке возрастания: $x_1 = -3$, $x_2 = -2$, $x_3 = 3$, $x_4 = 4$.
В данном случае никаких дополнительных проверок не требуется, поскольку как только значение трехчлена равно $\pm 3$, его абсолютная величина равна 3 без всяких дополнительных условий.
Замечание. В уравнении вида $|f(x)| = g(x)$, где $g(x)$ – переменная, область значений которой включает отрицательные числа, замена на $f(x) = \pm g(x)$ не является эквивалентной, так как полученное уравнение содержит также корни уравнения $|f(x)| = -g(x)$. Лишние корни можно исключить проверкой на $g(x) \geqslant 0$. См. решение уравнения $\eqref{eq:3.1.3}$ ниже.
Перейдем теперь от уравнения к неравенству:
$$
|x^2-x-9| \leqslant 3
$$
Теперь без интервалов не обойтись, но и здесь все не так скучно, как может показаться вначале.
Запишем неравенство в виде:
$$
p(x) = |x^2-x-9| - 3 \leqslant 0
$$
Корни $p(x)$ нам уже известны. Так как при этом ни один из корней не является кратным, то в каждом из них функция $p(x)$ меняет знак на противоположный.
Заметив, что $p(0) = 6 > 0$, можно расписать знаки на каждом промежутке:

Ответ: $[-3, -2] \cup [3,4]$. В случае строго неравенства, концы отрезков следует исключить (то есть отрезки заменяются интервалами),
а при смене знака неравенства используется дополнительное множество с учетом строгости неравенства. Например, решением неравенства $|x^2-x-9| \gt 3$
является множество $(-\infty, -3) \cup (-2, 3) \cup (4, +\infty)$.
Для возможных скептиков, которых предложенный метод недостаточно убедил, приведу также графическое решение. Рассмотрим многочлен $q(x)=x^2-x-9$,
стоящий под знаком абсолютной величины Так как его свободный член отрицателен, то дискриминант положителен. Таким образом его график пересекает ось абсцисс в двух точках. Так как его старший коэффициент положителен, график направлен острием вверх. Учитывая метод построения графика абсолютной величины, изложенный в главе 1.4, приходим к выводу, что график функции $|q(x)|$ выглядит так как указано на чертеже внизу красным цветом.

График функции $p(x)=|q(x)|-3$ (изображенный зеленым цветом) получается сдвигом на 3 единицы вниз, что дает уже не два, а четыре корня, значения которых нам известны. Знаки в промежутках между ними можно определить по графику. Заметим, что точно строить график не требуется, важно только понять, как он выглядит.
Тригонометрическое уравнение:
$$
|sin(3x)| = |sin(5x)| \label{eq:3.1.2}\tag{3.1.2}
$$
Полный улёт?! Но ведь нам хорошо известно, что абсолютные величины чисел равны тогда и только тогда, когда сами числа равны или противоположны. Отсюда получаем равносильное уравнение (вернее два уравнения, но постараемся их не разлучать, насколько это возможно):
$$
sin(3x) = \pm sin(5x)
$$
или
$$
sin(3x) \pm sin(5x) = 0
$$
Так и напрашивается перевести сумму-разность в произведения, используя формулы:
$$
sin\,\alpha \pm \sin\,\beta = 2\,sin\left(\dfrac{\alpha \pm \beta}{2}\right)\;cos\left(\dfrac{\alpha \mp \beta}{2}\right)
$$
Получаем уравнения:
$$
\begin{array}{l}
sin(4x)\;cos(x) = 0 \\
sin(x)\;cos(4x) = 0 \\
\end{array} \label{eq:3.1.2a}\tag{3.1.2a}
$$
Вместо того, чтобы приравнивать каждый сомножитель к нулю, перемножим эти уравнения. Корнями полученного уравнения
$$
sin(x)\,cos(x)\,sin(4x)\,cos(4x) = 0 \label{eq:3.1.2b}\tag{3.1.2b}
$$
являются те и только те числа, которые удовлетворяют одному из уравнений $\eqref{eq:3.1.2a}$, поэтому уравнение $\eqref{eq:3.1.2b}$
равносильно исходному уравнению $\eqref{eq:3.1.2}$.
Согласно формуле синуса двойного угла, уравнение $\eqref{eq:3.1.2b}$ в свою очередь сводится к уравнению:
$$
sin(2x)\,sin(8x) = 0
$$
Наконец, замечаем, что если $sin(2x)=0$, то
$$
sin(8x) = 2\;sin(4x)\;cos(4x) = 4\;sin(2x)\;cos(2x)\;cos(4x) = 0
$$
Поэтому достаточно решить уравнение
$$
sin(8x) = 0
$$
которое, которое, как ни трудно в это поверить, также равносильно исходному уравнению.
Несмотря на кажущиеся трудности, перебора практически удалось избежать.
Ответ: $x = \dfrac{\pi\,k}{8}$, $k=0, \pm1, \pm2, \dots$.
В предыдущем уравнении уберем знак абсолютной величины в правой части:
$$
|sin(3x)| = sin(5x) \label{eq:3.1.3}\tag{3.1.3}
$$
На первый взгляд этого уравнение упростилось, но взглянем более пристально. Теперь «метод $\pm$» следует применять с осторожностью. Дело в том, что уравнение $sin(3x) = \pm sin(5x)$ не равносильно уравнению $\eqref{eq:3.1.3}$, так как помимо нужных корней содержит также корни уравнения
$$
sin(3x) = -sin(5x) \label{eq:3.1.3a}\tag{3.1.3a}
$$
При этом из уравнения $\eqref{eq:3.1.3}$ следует $sin(5x) \geqslant 0$, тогда как в случае уравнения $\eqref{eq:3.1.3a}$ имеем $sin(5x) \leqslant 0$. Таким образом корни c положительным $sin(5x)$ оставляем, корни с отрицательным $sin(5x)$ отбрасываем, корни с $sin(5x)=0$ (если такие найдутся) также оставляем, так как они удовлетворяют обоим уравнениям, обращая их обе части в нуль.
Из решения предыдущего уравнения мы знаем, что решения уравнения $\eqref{eq:3.1.3}$ находятся среди корней уравнения $sin(8x)=0$. Так как $2\pi$ является общим периодом функций $sin(8x)$ и $sin(5x)$, следует среди предыдущих решений $x=\dfrac{\pi k}{8}$ выбрать значения, попадающие в полуинтервал длиной $2\pi$, для которых $\sin(5x) \geqslant 0$, а затем, прибавив к ним период $2\pi k$, получить все решения уравнения $\eqref{eq:3.1.3}$. В качестве интервала удобно взять $(-\pi, \pi]$, поскольку виду нечетности функций $sin(5x)$ и $sin(8x)$ достаточно рассмотреть неотрицательные значения x, при этом если $sin(5x) \geqslant 0$ выбираем $x$, в противном случае выбираем $-x$
Итак, просматриваем знаки $\sin(5x)$ для $x=\dfrac{\pi k}{8}$, попадающих в промежуток $[0, \pi]$. Выбранные корни обозначаются через $\xi_k$:
$$
\begin{array}{lllll}
k=0 & x=0 & 5x = 0 & sin(5x) = 0 & \xi_0 = 0 \\
k=1 & x=\frac{\pi}{8} & 5x=\frac{5\pi}{8} = \pi - \frac{3\pi}{8} & sin(5x) \gt 0 & \xi_1=\frac{\pi}{8} \\
k=2 & x=\frac{\pi}{4} & 5x=\frac{5\pi}{4} = \pi + \frac{\pi}{4} & sin(5x)\lt 0 & \xi_2=-\frac{\pi}{4} \\
k=3 & x=\frac{3\pi}{8} & 5x=\frac{15\pi}{8} = 2\pi - \frac{\pi}{8} & sin(5x)\lt 0 & \xi_3=-\frac{3\pi}{8} \\
k=4 & x=\frac{\pi}{2} & 5x=\frac{5\pi}{2} = 2\pi + \frac{\pi}{2} & sin(5x)\gt 0 & \xi_4=\frac{\pi}{2} \\
k=5 & x=\frac{5\pi}{8} & 5x=\frac{25\pi}{8} = 3\pi + \frac{\pi}{8} & sin(5x)\lt 0 & \xi_5=-\frac{5\pi}{8} \\
k=6 & x=\frac{3\pi}{4} & 5x=\frac{15\pi}{4} = 4\pi - \frac{\pi}{4} & sin(5x)\lt 0 & \xi_6=-\frac{3\pi}{4} \\
k=7 & x=\frac{7\pi}{8} & 5x=\frac{35\pi}{8} = 4\pi + \frac{3\pi}{8} & sin(5x)\gt 0 & \xi_7=\frac{7\pi}{8} \\
k=8 & x=\pi & 5x= 5\pi & sin(5x) = 0 & \xi_8=\pi
\end{array}
$$
Объединяя решения, используя при необходимости регулятор знака, получаем следующее:
$$
\left.
\begin{array}{l}
x_1 = \pi k \qquad (\xi_0, \; \xi_8) \\
x_2 = (-1)^k \dfrac{\pi}{8} + \pi k \qquad (\xi_1, \; \xi_7) \\
x_3 = (-1)^{k+1} \dfrac{\pi}{4} + \pi k \qquad (\xi_2, \; \xi_6) \\
x_4 = (-1)^{k+1} \dfrac{3\pi}{8} + \pi k \qquad (\xi_3, \; \xi_5) \\
x_5 = \dfrac{\pi}{2} + 2 \pi k \qquad (\xi_4)
\end{array}
\right\} \; k = 0, \pm1, \pm2, \dots
$$
Хочется пожелать, чтобы тригонометрическое уравнение подобного рода вам никогда не попадалось.😊
Тригонометрическое неравенство:
$$
2|cos\,x| - 1 \lt sin\,x \label{eq:3.1.4}\tag{3.1.4}
$$
Когда абсолютная величина присутствует в одном экземпляре, рекомендуется ее оставить в гордом одиночестве. В данном случае следует перенести $1$ вправо:
$$
2|cos\,x| \lt 1 + sin\,x \label{eq:3.1.4a}\tag{3.1.4a}
$$
Так как $sin \,x \geqslant -1$, обе части неравенства $\eqref{eq:3.1.4a}$ заведомо неотрицательны. Это позволяет возвести неравенство в квадрат,
напрочь забыв об абсолютной величине:
$$
4\;cos^2x \lt 1 + 2\,sin\,x + sin^2x
$$
Очевидная замена $cos^2x = 1-sin^2x$ приводит к неравенству
$$
5\,sin^2x+2\,sin\,x-3 \gt 0
$$
которое после подстановки $t=sin\,x$ становится квадратным:
$$
5t^2 + 2t-3 \gt 0
$$
Решение неравенства распадается на два интервала $t \in (-\infty, -\frac{3}{5}) \cup (1, +\infty)$, однако второй интервал отпадает,
так как заведомо $sin\,x \leqslant 1$. Таким образом приходим к неравенству:
$$
sin\,x \lt -\frac{3}{5}
$$
которое решается стандартным способом.
Ответ: $arcsin(\frac{3}{5}) + \pi(2k-1) \lt x \lt - arcsin(\frac{3}{5}) + 2\pi k$, $k=0, \pm1, \pm2, \dots$.
И, наконец, простенькая система уравнений, которая тем не менее оказалась в некогда весьма популярном задачнике (В.Б.Лидский, Л.В.Овсянников, А.Н.Тулайков, М.И.Шабунин. Задачи по элементарной математике, М.Наука 1969, задача 42):
$$
\begin{cases}
|x-1| + |y-5| = 1 \\
y = 5 + |x-1|
\end{cases} \label{eq:3.1.5}\tag{3.1.5}
$$
Достаточно в нижнем уравнении переместить $5$ влево,
$$
y-5 = |x-1| \label{eq:3.1.5a}\tag{3.1.5a}
$$
как становится ясным, что $y-5 \geqslant 0$, поэтому в верхнем уравнении знак абсолютной величины во втором слагаемом можно опустить:
$$
|x-1| + (y-5) = 1 \label{eq:3.1.5b}\tag{3.1.5b}
$$
Более того, от абсолютной величины можно полностью избавиться, если поставить выражение для $|x-1|$ из $\eqref{eq:3.1.5a}$ в $\eqref{eq:3.1.5b}$:
$$
(y-5) + (y-5) = 1 \; \Rightarrow \; y-5 = 0,5 \; \Rightarrow \; y = 5,5
$$
Далее из $|x-1| = y-5 = 0,5$ получаем: $x = 1 \pm 0,5$
Ответ: $x_1 = 1,5$, $x_2 = 0,5$, $y_1 = y_2 = 5,5$.
3.2. Когда перебор интервалов уместен или неизбежен
Зачастую перебор исключить невозможно, или его использование предпочтительнее альтернативных методов. Рассмотрим такие случаи.
Показательное уравнение:
$$
5^{|4x-6|} = 25^{3x-4} \label{eq:3.2.1}\tag{3.2.1}
$$
Из вступительного на факультет вычислительной математики и кибернетики МГУ 1979 года. Казалось бы задача более уместна для химфака или биофака. Однако, если предлагать только архисложные задачи, то, может статься, выбирать будет не из кого 😊
На самом деле, наличие показательных функций является лишь отвлекающим маневром. Достаточно заметить, что
$$
5^{|4x-6|} = 5^{2\cdot|2x-3|} = 25^{|2x-3|}
$$
что приводит к уравнению $25^{|2x-3|} = 25^{3x-4}$, которое, ввиду однозначности показательной функции сводится к
$$
|2x-3|=3x-4 \label{eq:3.2.1a}\tag{3.2.1a}
$$
Пытаясь обойтись без перебора, заметим, что неотрицательность правой части дает $x \in \left[\frac{4}{3}, +\infty\right)$, тогда как точка излома абсолютной
величины (соответствующая $2x-3=0$), равная $\frac{3}{2}$, разбивает полуинтервал $x \in \left[\frac{4}{3}, +\infty\right)$ на два полуинтервала:
$\left[\frac{4}{3}, \frac{3}{2}\right)$ и $\left[\frac{3}{2}, +\infty\right)$.
Увы, в этот раз получилось на так гладко, как хотелось бы. Всё-таки можно исключить перебор, если возвести $\eqref{eq:3.2.1a}$ в квадрат, а затем исключить возможные корни меньшие $\frac{4}{3}$, как лишние. Однако квадратное уравнение внесет даже бо́льшую энтропию, чем перебор, к тому же не каждому экзаменатору это может понравиться.
Поэтому будем решать «каноническим» способом, и заодно покажем, как это делается.
Имеем:
$$
|2x-3| =
\begin{cases}
2x-3, \quad \text{при} \quad x \geqslant \frac{3}{2} \\
3-2x, \quad \text{при} \quad x \lt \frac{3}{2} \\
\end{cases}
$$
что приводит к двум уравнениям
$$
\begin{align}
2x-3 = 3x-4, \quad & x \geqslant \frac{3}{2} \\
3-2x = 3x-4, \quad & x \lt \frac{3}{2}
\end{align}
$$
Перенося все слагаемые влево приводя подобные и умножая на $(-1)$, получаем:
$$
\begin{align}
x-1 = 0, \quad & x \geqslant \frac{3}{2} \\
5x-7 = 0, \quad & x \lt \frac{3}{2}
\end{align}
$$
Здесь можно (хотя и не обязательно) подстраховаться и проверить, что выражения в левой части принимают одинаковые значения в точке излома,
что следует из непрерывности абсолютной величины: $\frac{3}{2} - 1 = \frac{1}{2}$, $5\cdot\frac{3}{2}-7 = \frac{15}{2} - 7 = \frac{1}{2}$. Все в порядке!
Первое уравнение дает: $x=1$, что не удовлетворяет неравенству $x \geqslant \frac{3}{2}$.
Из второго уравнения получаем:
$x = \frac{7}{5}$. Так как $\frac{7}{5} = 1,4 \lt 1,5 = \frac{3}{2}$, условие $x \lt \frac{3}{2}$ выполнено, и корень подходит.
Ответ: $x= \dfrac{7}{5} = 1,4$.
Неравенство:
$$
|x^3-8| \leqslant x^3 + x + 8 \label{eq:3.2.2}\tag{3.2.2}
$$
Источник: Е.Ваховский, А.Волынский «Научимся обращаться с абсолютной величиной» Квант №9, 1972
Если кубический трехчлен в правой части имеет рациональный корень, он должен быть целым, отрицательным и делителем 8. Проверяем
(-1), (-2) — безуспешно, тогда как на числа (-4) и (-8) даже нет смысла тратить время.
Поскольку корни трехчлена в правой части найти не удается, придется сразу перейти к исследованию выражения под знаком абсолютной величины. Уравнение $x^3 - 8 = 0$ в области вещественных чисел (а именно такие числа имеются в виду, так как к комплексным числам знак ⩽ не применим) имеет единственный корень $x=2$, при этом:
$$
|x^3 - 8| = \begin{cases}
x^3 - 8 \quad \text{при} \quad x \geqslant 2 \\
8 - x^3 \quad \text{при} \quad x \lt 2
\end{cases}
$$
что дает две системы неравенств:
|
$$
\begin{cases}
x \geqslant 2 \\
x^3 - 8 \leqslant x^3 + x + 8
\end{cases}
$$
|
|
\begin{cases}
x \lt 2 \\
8 - x^3 \leqslant x^3 + x + 8
\end{cases}
|
упрощая которые получаем:
|
$$
\begin{cases}
x \geqslant 2 \\
x \geqslant -16
\end{cases}
$$
|
|
\begin{cases}
x \lt 2 \\
2x^3 + x \geqslant 0
\end{cases}
|
Система неравенств слева совместна, общий результат: $x \geqslant 2$.
В системе неравенств справа второе неравенство можно записать, как $x(2x^2 + 1) \geqslant 0$ и, так как выражение в скобках заведомо положительно,
эта система неравенств сводится к
$$
\begin{cases}
x \lt 2 \\
x \geqslant 0
\end{cases}
$$
которая несовместна.
Ответ: $x \in [2,+\infty)$
Логарифмическое уравнение:
$$
\left| \frac{\ln(2-x)}{\ln(x)} \right|= 2 \label{eq:3.2.3}\tag{3.2.3}
$$
Особенность этого уравнения состоит в том, что выражение слева имеет смысл при далеко не всех значениях $x$. Во-первых, выражение под знаком логарифма должно быть положительным, а так как логарифмов у нас аж два, получаем двойное неравенство $0 \lt x \lt 2$. Во-вторых, знаменатель не должен быть нулем, то есть $x \ne 1$, поэтому единицу следует выколоть из полученного интервала. Получаем таким образом:
$$
x \in (0,1) \cup (1, 2) \label{eq:3.2.3a}\tag{3.2.3a}
$$
Далее идем по проторенной дорожке, благо правая часть является константой:
$$
\begin{array}{l}
\dfrac{\ln(2-x)}{\ln(x)}= \pm 2 \; \Rightarrow \; \ln(2-x) = \pm 2\,\ln(x) \; \Rightarrow \; \ln(2-x) = \ln(x^{\pm 2})
\end{array}
$$
и ввиду однозначности логарифма от него можно избавиться:
$$
2-x = x^{\pm 2}
$$
И всё же наследие логарифмов дает о себе знать: придется, к сожалению, рассматривать два случая:
$$
\begin{array}{l}
1) 2-x = x^2 \quad \Leftrightarrow \qquad x^2 - x + 2 - 0 \\
2) 2-x = \frac{1}{x^2} \quad \Leftrightarrow \quad x^3 - 2\,x^2 + 1 = 0
\end{array}
$$
Утешает лишь то, что здесь нет нудных специфических условий — достаточно лишь проверить, что решение удовлетворяет $\eqref{eq:3.2.3a}$.
Из первого уравнения находим: $x_1 = 1, x_2 = -2$. При этом от обоих корней приходится отказаться, так как один из них обращает знаменатель в нуль, а при другом логарифм теряет смысл.
Второе уравнение является кубическим, однако, к счастью, оно имеет легко угадываемый корень: $x=1$, что позволяет разложить соответствующий кубический трехчлен на множители (конечно, можно было применить схему Гoрнера (Horner), однако автор этих строк забыл, как ей пользоваться — случается и такое!):
$$
x^3 - 2\,x^2 + 1 = (x^3 - x^2) - (x^2 - 1) = x^2(x-1) - (x+1)(x-1) = (x-1)(x^2-x-1)
$$
и поскольку значение $x=1$ не является допустимым, остается лишь надеяться на трехчлен $x^2-x-1$ с (увы!) иррациональными корнями.
Получаем: $x = \dfrac{1 \pm \sqrt{5}}{2}$, где корень с минусом отбрасывается, как отрицательный, и остается попытать счастья с $\dfrac{\sqrt{5}+1}{2}$. Из $4 \lt 5 \lt 9$ получаем $2 \lt \sqrt{5} \lt 3$, откуда $\dfrac{3}{2} \lt \dfrac{\sqrt{5}+1}{2} \lt 2$, так что решение комфортабельно входит в требуемый интервал.
Ответ: $x= \dfrac{\sqrt{5}+1}{2}$.
Между прочим, полученный результат — это в точности золотое сечение (англ. golden ratio), за что ему можно даже простить иррациональность.😊
А не слишком ли жестоко мы обошлись с единицей, исключив ее из допустимых значений? Ведь при $x=1$, числитель левой части уравнения $\eqref{eq:3.2.3}$ также обращается в нуль, приводя к неопределенности $\frac{0}{0}$. Поэтому возможно удастся до-определить функцию в единице, так чтобы она стала непрерывной, после чего единица перестанет быть изгоем. Вычислим предельное значение с помощью правила Лопиталя (l'Hôpital, лат. l'Hospital):
$$
\lim\limits_{x \to 1}\frac{\ln(2-x)}{\ln(x)} = - \lim\limits_{x \to 1} \frac{x}{2-x} = -1
$$
так что $\lim\limits_{x \to 0} \left| \dfrac{\ln(2-x)}{\ln(x)} \right| = 1$, тогда как требуется 2. Все-таки не зря мы исключили единицу!
И наконец, неравенство с тремя знаками абсолютной величины:
$$
|3x-1| + |x+2| > |4-x| + 20 \label{eq:3.2.4}\tag{3.2.4}
$$
Три знака абсолютной величины, четыре числовых промежутка — ну это уже слишком! Но вместо того, чтобы сокрушаться, будем рассуждать логически.
Так как переменная везде появляется лишь в первой степени, график функции между соседними точкам излома является отрезком прямой, и
если в этих точках знак функции одинаков, то между ними знак не может меняться при всем его желании.
Итак, переносим все слагаемые влево, чтобы понять, о какой функции идет речь. Заодно, во избежание путаницы, заменим $|4-x|$ на $|x-4|$:
$$
p(x) = |3x-1| + |x+2| - |x-4| - 20 \gt 0 \label{eq:3.2.4a}\tag{3.2.4a}
$$
Выпишем точки излома в порядке возрастания: $-2, \frac{1}{3}, 4$ и найдем значения левой части неравенства $\eqref{eq:3.2.4a}$ в этих точках:
$$
\begin{array}{l}
p(-2) = 7 + 0 - 6 - 20 = -19 \lt 0 \\
p(\frac{1}{3}) = 0 + 2\frac{1}{3} - 3\frac{2}{3} - 20 = -21\frac{2}{3} \lt 0 \\
p(4) = 11 + 6 + 0 - 20 = -3 \lt 0
\end{array}
$$
Таким образом, во всех точках излома значения функции отрицательны. Выходит, функция нигде не бывает положительной?
Но ведь мы не учли крайние, бесконечные интервалы: $(-\infty, -2)$ и $(4, +\infty)$. Итак, рассмотрим их и только иx!
Получаем две системы неравенств:
|
$$
\begin{cases}
x \lt -2 \\
1-3x-x-2-4+x-20 \gt 0 \quad \Leftrightarrow \quad -3x-25 \gt 0
\end{cases}
$$
|
|
\begin{cases}
x \gt 4 \\
3x-1+x+2-x+4-20 \gt 0 \quad \Leftrightarrow \quad 3x-15 \gt 0
\end{cases}
|
или
|
$$
\begin{cases}
x \lt -2 \\
x \lt -\frac{25}{3} = -8\frac{1}{3}
\end{cases}
$$
|
|
\begin{cases}
x \gt 4 \\
x \gt 5
\end{cases}
|
Ответ: $x \in \left(-\infty, -8\frac{1}{3}\right) \cup (5, +\infty)$.
ЗАДАЧИ
Часть 1
1.1Докажите, что если $|x|\lt 1$, $|y| \lt 1$, то $\left|\dfrac{x-y}{1-xy}\right| \lt 1$.
1.2Даны три приведённых (коэффициент при $x^2$ равен 1) квадратных трехчлена: $P_1(x)$, $P_2(x)$ и $P_3(x)$ коэффициентами.
Докажите, что уравнение $|P_1(x)| + |P_2(x)| = |P_3(x)|$ имеет не более восьми корней.
1.3Какие из нижеследующих функций вещественного переменного $x$ являются неограниченными:
a) $2^{-|x|}$, b) $\dfrac{|x|}{x}$, c) $\lg |sin\,x|$ d) $\left|\dfrac{sin(2x) - sin\,6}{x-3}\right|$
1.4Найти первообразную функции $y=|x|$ ($x$ - вещественный аргумент). Построить график функции $y=\int\limits_0^x{|t|dt}$.
1.5Верно ли равенство $|\sqrt[n]{z}| = \sqrt[n]{|z|}$ для комплексных чисел?
1.6$z_1$ и $z_2$ — комплексные числа. Докажите, что $|z_1-z_2|$ является расстоянием между точками комплексной плоскости, соответствующими этим числам.
1.7$z_1$ и $z_2$ — комплексные числа. Известно, что $|z_1+z_2| = 10$, $|z_1-z_2| = 4$, $|z_1| = 6$. Найти $|z_2|$.
1.8M - множество комплексных чисел, удовлетворяющих неравенству $|z+3+4i| \leqslant 6$.
a) Найти минимальное и максимальное значение |z| на этом множестве;
b) Найти числа, соответствующие минимальному и максимальному значению |z|
c) Найти минимальную величину $|z-2-8i|$ для $z \in M$, и соответствующее значение $z$
1.9Разность $\sqrt{|12\sqrt{5}-29|} - \sqrt{12\sqrt{5}+29}$ является целым числом. Найти это число.
Решения задач части 1
Часть 2
Решить в области вещественных чисел
2.1$||5-2x|-1| = 4$.
2.2$|sin\,x| = cos\,x$.
2.3$|sin\,x| \gt cos\,x$.
2.4$|x^4-x^2-5| = ||x^4-4|-x^2-1|$.
2.5$|x-2|+|x-1|+|x|+|x+1|+|x+2| \leqslant 6$.
2.6$x^2\cdot2^{x+1}+2^{|x-3|+2} = x^2\cdot2^{|x-3|+4}+2^{x-1}$.
2.7$\begin{cases}|x+y| = 1 \\ |x|+|y| = 3\end{cases}$
2.8$\begin{cases}|x+3|+|y+1| = 4 \\ |x-1|+|y-3| = 5\end{cases}$
2.9$|\sqrt{2}|x|-1| \cdot \log_2{(2-2x^2)} \geqslant 1$
2.10$\dfrac{4}{|x+1|-2} \geqslant |x-1|$
Решения задач части 2
Часть 3
Построить графики функций вещественного переменного:
3.1$y=|\sqrt{|x+2|}-1|$
3.2$y=\dfrac{|x+2|}{|x-1|}$
3.3$y=|2x+1|-|x+5|+|x+1|-|2x-5|$
3.4$y=x^2-5|x-1|+5$
Построить множество точек координатной плоскости, удовлетворяющих неравенству:
3.5$|y+1|+|x-4| \lt x$.
3.6$x^2+y^2+x\cdot|x|+y\cdot|y| \gt 8$.
Решить в области комплексных чисел.
3.7$|z-2+3i| = |4+i\sqrt{3}|$.
3.8$||z-2|-(7+4i)||\leqslant 5$.
3.9$z^2-5|z|+6 = 0$.
Решения задач части 3
Часть 4
4.1Для положительных параметров $a$ и $b$ построить множество точек координатной плоскости,
удовлетворяющих неравенству $\frac{|x|}{a}+\frac{|y|}{b} \leqslant 1$. Вычислить его площадь. А если заданное неравенство заменить
неравенством $\left|\frac{x}{a}+\frac{y}{b}\right| \leqslant 1$?
4.2Сколько целочисленных пар $(x,y)$ удовлетворяет соотношениям ($n$ - целое неотрицательное число):
a) $|x|+|y| = n$;
b) $|x|+|y| \leqslant n$;
4.3Определить наибольшее и наименьшее значение выражения $(x^2-6x+y^2)$ на множестве чисел,
задаваемом неравенством $|x-y|+|x+y| \leqslant 2$.
1.4Для каких вещественных значений $a$ существует вещественное $b$, удовлетворяющее неравенствам $|7a − 3b| \leqslant 1$ и $|5a + 7b| \leqslant 1$?
4.5Найти площадь множества точек $z$ комплексной плоскости, удовлетворяющих неравенству $|z+3+2i| + |z-5-4i| \lt 12$.
4.6Определить, при каких значениях вещественного $a$:
а) неравенство $3-|x-a| \gt x^2$ имеет хотя бы одно отрицательное решение
b) неравенство $2 \gt |x+a|+x^2$ имеет хотя бы одно положительное решение
4.7Докажите, что если для вещественных чисел $a$, $b$ и $c$ выполняются неравенства $|a-b| \geqslant |c|$, $|b-c| \geqslant |a|$, $|c-a| \geqslant |b|$, то хотя бы одно из этих чисел равно сумме двух других.
4.8Докажите, что если разность между наибольшим и наименьшим из $n$ вещественных чисел $a_1$, $a_2$, ... $a_n$
равна $d$ (т.е. $d=\max\limits_{i \lt j}|a_i-a_j|$), a $s$ — сумма модулей всех попарных разностей этих чисел ($s=\sum\limits_{i \lt j}{|a_i-a_j|}$),
то $(n-1)d \leqslant s \leqslant \frac{n^2}{4}d$.
4.9Докажите, что если множество вещественных чисел
$$
\begin{matrix}
a_{11},\; a_{12},\; \dots, \; a_{1n}\\
a_{21},\; a_{22},\; \dots, \; a_{2n}\\
.\;.\;.\;.\;.\\
a_{n1},\; a_{n2},\; \dots, \; a_{nn}
\end{matrix}
$$
для некоторого положительного $M$ удовлетворяет неравенствам
$$
\sum\limits_{i=1}^{n}|a_{i1}\cdot x_1 + a_{i2} \cdot x_2 + \dots + a_{in}\cdot x_n| \leqslant M
$$
для любого набора $\{x_1,\dots, x_n\}$ из чисел, равных $\pm 1$ (другими словами $|x_k|=1$, $k=1,2,\dots, n$), то справедлива оценка
$$
|a_{11}|+|a_{22}|+\dots+|a_{nn}| \leqslant M
$$
Решения задач части 4