Описание и условия задач

Решения задач части 1

Решения задач части 2

Решения задач части 3

Решения задач части 4

 

4.1Для положительных параметров $a$ и $b$ построить множество точек координатной плоскости, удовлетворяющих неравенству $\frac{|x|}{a}+\frac{|y|}{b} \leqslant 1$. Вычислить его площадь. А если заданное неравенство заменить неравенством $\left|\frac{x}{a}+\frac{y}{b}\right| \leqslant 1$?

Функция $f(x,y)=\frac{|x|}{a}+\frac{|y|}{b}$ является четной относительно $x$ и $y$: $f(-x,y)$ = $f(x,-y)$ = $f(x,y)$. Поэтому достаточно построить искомое множество точек в первом квадранте (т.е. для неотрицательных $x$ и $y$) а затем распространить множество на другие квадранты зеркальным отражением относительно осей координат.

В первом квадранте неравенство записывается, как $$ \frac{x}{a}+\frac{y}{b} \leqslant 1 \label{eq:4.1.1}\tag{4.1.1} $$ или $$ y \leqslant -\dfrac{b}{a}\,x + b \label{eq:4.1.2}\tag{4.1.2} $$

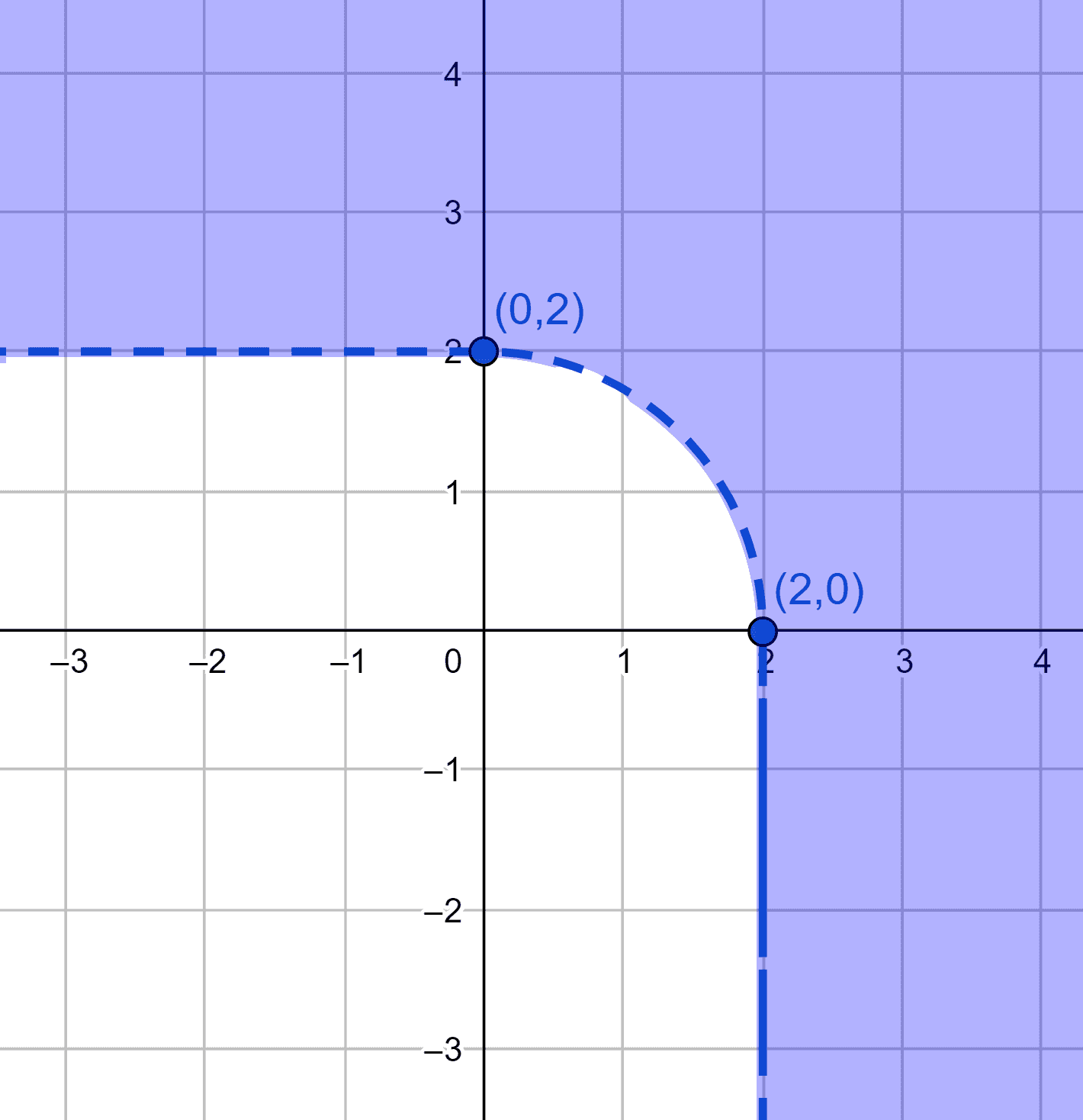
Отсюда понятно, что искомое множество образуют точки, расположенные на и ниже прямой линии задаваемой уравнением $\eqref{eq:4.1.2}$. Подставляя нулевые значения $x$ и $y$ в $\eqref{eq:4.1.1}$, находим точки пересечения прямой с координатными осями: $(a, 0)$, $(0, b)$, что позволяет построить множество точек.

В построенном множестве следует выбрать область, находящуюся в первом квадранте. Такой областью является прямоугольный треугольник (включая его контур), вершиной прямого угла которого является начало координат.

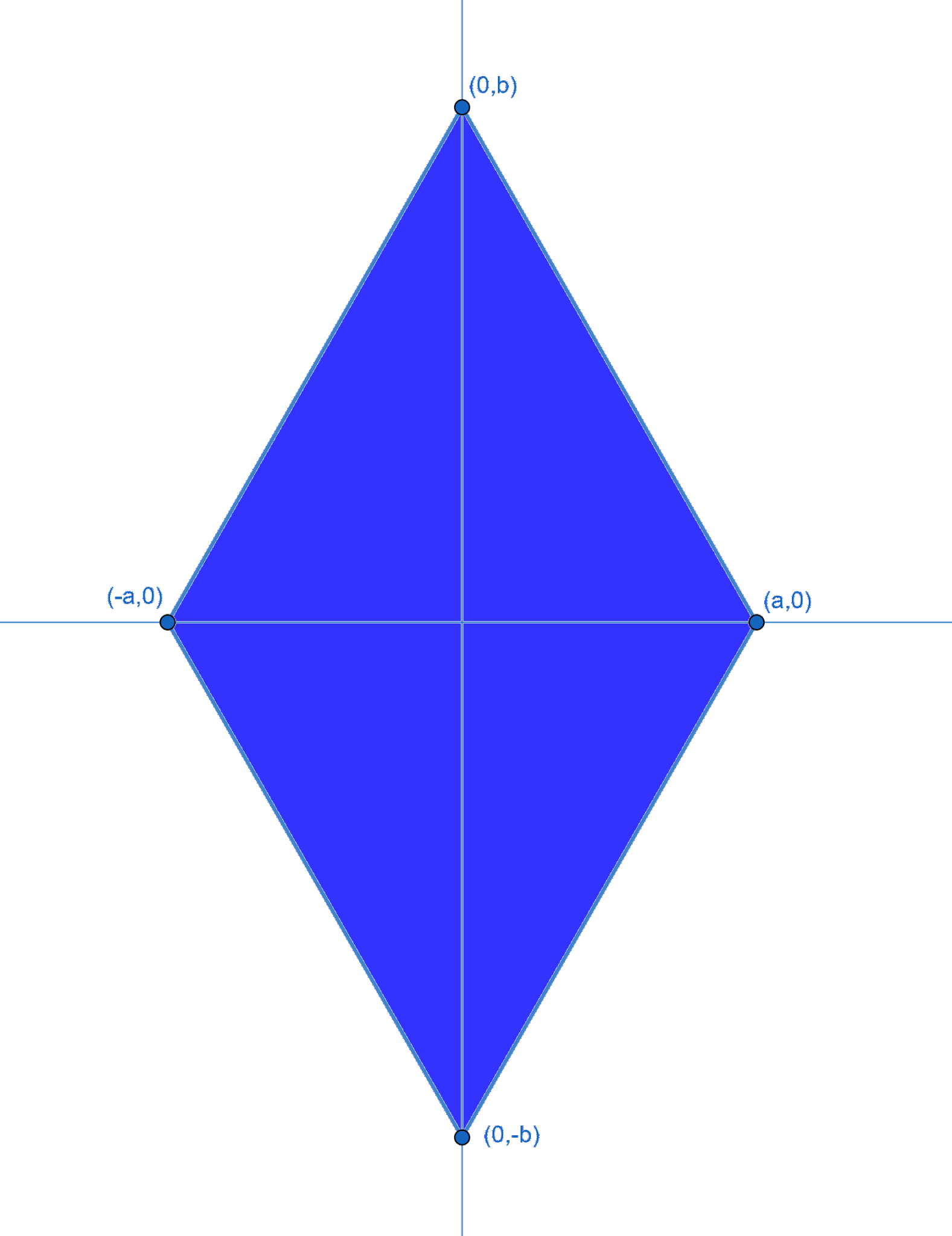
Распространяя полученный треугольник на другие квадранты, получаем ромб, с вершинами в точках $(a, 0)$, $(0, b)$, $(-a, 0)$, $(0, -b)$. Полученный ромб является множеством точек, удовлетворяющих неравенству $\frac{|x|}{a}+\frac{|y|}{b} \leqslant 1$

Площадь множества находим, как полупроизведение его диагоналей: $$ S = \frac{1}{2} \cdot 2a \cdot 2b = 2ab $$

$\frac{x}{a}+\frac{y}{b} \leqslant 1$

$\frac{|x|}{a}+\frac{|y|}{b} \leqslant 1$

$\left|\frac{x}{a}+\frac{y}{b}\right| \leqslant 1$

 

Неравенство $\left|\frac{x}{a}+\frac{y}{b}\right| \leqslant 1$ можно переписать как $$ -1 \leqslant \frac{x}{a}+\frac{y}{b} \leqslant 1 $$ или $$ -\dfrac{b}{a}\,x - b \leqslant y \leqslant -\dfrac{b}{a}\,x + b $$

Соответствующее множество точек расположено ниже уже знакомого нам графика функции $y=-\dfrac{b}{a}\,x + b$ и выше графика функции $y=-\dfrac{b}{a}\,x - b$, получающегося сдвигом на $2b$ единиц вниз, включая ограничивающие линии. Такое множество неограничено.

4.2Сколько целочисленных пар $(x,y)$ удовлетворяет соотношениям ($n$ - целое неотрицательное число):
   a) $|x|+|y| = n$;
   b) $|x|+|y| \leqslant n$;

Неравенство $|x|+|y| \leqslant n$ является частным случаем неравенства предыдущей задачи при $a=b=n$. Таким образом множеством точек координатной плоскости, соответствующих этому неравенству, является квадрат с вершинами в точках $(n,0)$, $(0,n)$, $(-n,0)$ и $(0,-n)$.

a) Подсчитаем количество точек с целочисленными координатами, находящихся на контуре квадрата.

Будем к каждой стороне квадрата относить ее внутренние точки с целочисленными координатами, а также левый конец, если смотреть изнутри квадрата. Например, к стороне лежащей в I-м квадранте относятся точки $(n,0)$, $(1,n-1)$, ... $(n-1,1)$, тогда как точка $(n,0)$ относится к стороне $IV$-го квадранта. В этом случае каждой стороне соответствует $n$ точек, так что общее количество точек равно $4n$

Заметим, что при $n=0$ формула дает нуль, тогда как на самом деле существует одна целочисленная пара $(x,y)$, удовлетворяющая уравнению $|x|+|y|=0$ — это конечно $(0,0)$.

Ответ: $M_k = \left\{\begin{array}{r} 1,\quad \text{если}\quad n=0 \\4n, \quad \text{если} \quad n \gt 0\end{array}\right.$,   или одной формулой: $M_k = (4n-1)sgn(x)+1$, где функция $sgn(x)$ определяется из (1.1.8).

b) Первый способ. Добавим к точкам контура точки внутри квадрата с целочисленными координатами. На оси абсцисс (то есть при $y=0$) содержится $(2n+1)$ точек с $x=0, \pm 1, \dots \pm n$. При каждом увеличении $|y|$ на единицу количество соответствующих точек уменьшается на 2.

Таким образом, имеется:

• $(2n+1)$ точек с $y= 0$
• $(2n-1)$ точек с $y= \pm 1$
• $(2n-3)$ точек с $y= \pm 2$
•      ...
• $3$ точки с $y= \pm (n-1)$
• $1$ точкa с $y= \pm n$

Отсюда общее количество точек c целочисленными координатами внутри и на контуре квадрата равно: $$ (2n+1) + 2\cdot [(2n-1) + (2n-3) + \dots + 3 + 1] = 2n+1 + 2 \cdot \dfrac{[(2n-1)+1]n}{2} = 2n^2+2n+1 = 2n(n+1)+1 $$

Полученная формула верна также при $n=0$.

Ответ: $2n(n+1)+1$.

Второй способ. Поскольку для целых $x$ и $y$ сумма $x$+$y$ всегда является целой, целочисленная пара $(x, y)$ удовлетворяет неравенству $|x|+|y| \leqslant n$ тогда и только тогда, когда она удовлетворяет уравнению $|x|+|y|=k$, при некотором целом $k \in [0, n]$, причем $k$ для каждой пары определяется единственным образом. Количество $M_k$ целочисленных решений уравнения $|x|+|y|=k$ было вычислено в пункте a).

Таким образом, искомое количество пар равно: $$ M_0 + M_1 + M_2 + \dots + M_n = 1 + 4 \cdot 1 + 4\cdot 2 + \dots + 4n = 1 + 4(1+2+\dots+n) = 1 + 4 \cdot \dfrac{n(n+1)}{2} = 2n(n+1) + 1 $$

Ответ: $2n(n+1)+1$.

4.3Определить наибольшее и наименьшее значение выражения $(x^2-6x+y^2)$ на множестве чисел, задаваемом неравенством $|x-y|+|x+y| \leqslant 2$.

American Math Competition, 2011г. В оригинале равенство вместо неравенства.

Если $x$ и $y$ одинакового знака или одно из них нуль, то $$ |x-y| = ||x|-|y||, \quad |x+y| = |x|+|y| \quad \Rightarrow \quad |x-y| + |x+y| = |x|+|y| + ||x|-|y|| $$

Если $x$ и $y$ разных знаков, то $$ |x-y| = |x|+|y|, \quad |x+y| = ||x|-|y|| \quad \Rightarrow \quad |x-y| + |x+y| = |x|+|y| + ||x|-|y|| $$

Таким образом, в любом случае левая часть заданного неравенства преобразуется к виду $|x|+|y| + ||x|-|y||$.

Но это еще не всё! Учитывая, что $||x|-|y|| = max(|x|-|y|, |y|-|x|)$, получаем: $$ |x|+|y| + ||x|-|y|| = |x|+|y| + max(|x|-|y|, |y|-|x|) = max(|x|+|y|+|x|-|y|, |x|+|y|+|y|-|x|) = max(2|x|, 2|y|) = 2\cdot max(|x|, |y|) $$ в результате чего заданное неравенство магически превращается в: $$ max(|x|,|y|) \leqslant 1 $$ что равносильно системе неравенств: $$ \begin{cases}|x|\leqslant 1 \\ |y| \leqslant 1 \end{cases} \label{eq:4.3.1}\tag{4.3.1} $$

Настало время заняться функцией $f(x,y)=x^2-6x+y^2$, что можно сделать аналитически или графически.

Аналитический метод. Понятно, что наибольшее значение функции на множестве, заданном системой $\eqref{eq:4.3.1}$, достигается при $y^2=1$, ($y = \pm 1$), а наименьшее при $y^2=0$ ($y=0$). Это дает две функции: $$ g_{max}(x) = x^2-6x+1, \qquad g_{min}(x) = x^2-6x $$

У графиков обоих функций вершина параболы находится в точке с $x=3$, то есть правее промежутка $[-1,1]$. Это значит, что при $|x| \leqslant 1$ обе функции монотонно убывают. Таким образом находим наибольшее и наименьшее значение $f(x,y)$ на заданном множестве пар $(x,y)$: $$ \begin{array}{l} f_{max} = g_{max}(-1) = 8 \quad соответствует \quad x=-1, \; y = \pm 1 \\ f_{min} = g_{min}(1) = -5 \quad соответствует \quad x=1, \; y = 0 \\ \end{array} $$

Графический метод.

Системе неравенств $\eqref{eq:4.3.1}$ соответствует множество точек координатной плоскости, ограниченное вертикальными прямыми $x = \pm 1$ и горизонтальными прямыми $y = \pm 1$. Таким множеством является квадрат, вершинами которого служат точки $A(-1,-1)$, $B(-1,1)$, $C(1,1)$ и $D(1,-1)$.

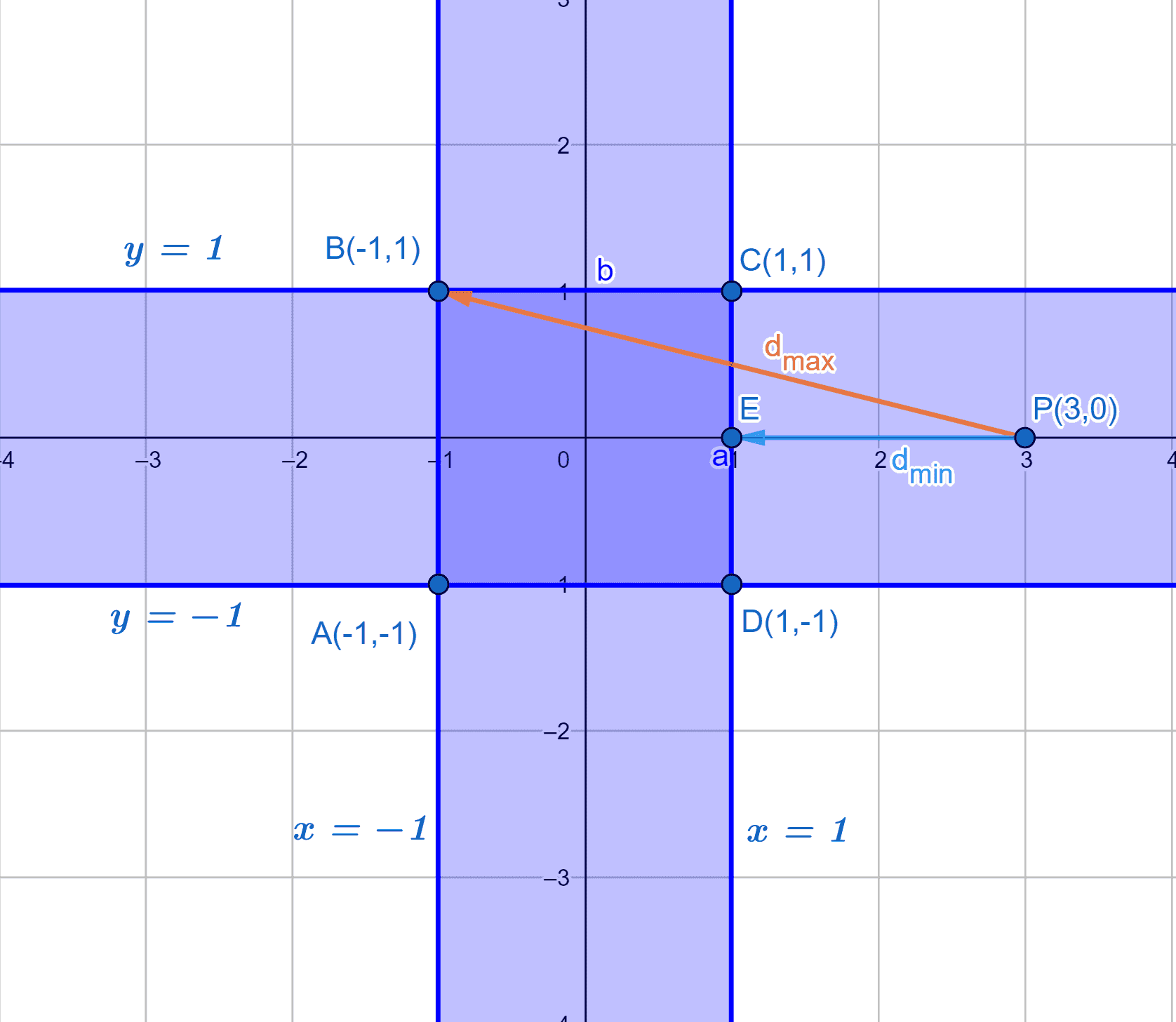
Выделив полный квадрат в функции $f(x,y)=x^2-6x+y^2$, получаем: $$ f(x,y) = (x-3)^2 + y^2 - 9 = d^2(x,y) - 9 $$ где $d(x,y) = \sqrt{(x-3)^2+y^2}$ — расстояние от точки с координатами $(x,y)$ до точки $P(3,0)$. Ввиду монотонного возрастания квадратного корня максимум и минимум функции $f(x,y)$ достигается там же, где и соответственно максимум и минимум $d(x, y)$. Таким образом задача свелась к следующей: найти точки квадрата $ABCD$, наиболее и наименее удаленные от точки $P$.

Как видно на чертеже, ближайшей к $P$ точкой квадрата является середина стороны $CD$ точка $E(1,0)$. Таким образом, $$ d_{min} = |3-1| = 2 $$. тогда как наиболее удаленными точками квадрата являются точки $A$ и $B$ с координатами $(-1,\pm1)$. Таким образом $$ d_{max} = \sqrt{[(3-(-1)]^2 + 1^2} = \sqrt{17} $$

Отсюда: $$ f_{max} = d_{max}^2 - 9 = 8 \qquad f_{min} = d_{min}^2 - 9 = -5 $$

Ответ: 8 и (-5).

Так просто, что даже не верится. Интересно, как решали задачу ее авторы.

4.4Для каких значений вещественных $a$ существует вещественное $b$, удовлетворяющее неравенствам $|7a − 3b| \leqslant 1$ и $|5a + 7b| \leqslant 1$?

Источник: Н.Б.Алфутова, Ю.Е.Егоров, А.В.Устинов. «18×18 Вступительные задачи ФМШ при МГУ.» М: МЦНМО, 2017», задача 3.15, стр, 43. В отличие от графического решения, подразумеваемого в указаниях оригинала, здесь приводится аналитический подход, который в данном случае представляется более простым.

Перепишем заданные неравенства, чтобы коэффициенты при $b$ были положительными: $$ \begin{cases} |3b-7a| \leqslant 1 \\ |7b+5a| \leqslant 1 \end{cases} \quad \Leftrightarrow \quad \begin{cases} -1 \leqslant 3b-7a \leqslant 1 \\ -1 \leqslant 7b+5a \leqslant 1 \end{cases} $$ или $$ \begin{cases} \;\;\,\dfrac{7}{3}a - \dfrac{1}{3} \leqslant b \leqslant \;\;\,\dfrac{7}{3}a + \dfrac{1}{3} \\ -\dfrac{5}{7}a - \dfrac{1}{7} \leqslant b \leqslant -\dfrac{5}{7}a + \dfrac{1}{7} \end{cases} $$

Для совместности полученной системы необходимо и достаточно, чтобы отрезки $\left[\frac{7}{3}a - \frac{1}{3}, \frac{7}{3}a + \frac{1}{3} \right]$ и $\left[-\frac{5}{7}a - \frac{1}{7}, -\frac{5}{7}a + \frac{1}{7} \right]$ пересекались. Осталось лишь это требование перевести на язык неравенств ... в чем однако можно увязнуть всерьез и надолго. Гораздо проще ответить на противоположный вопрос: когда отрезки не пересекаются. Это происходит когда либо первый отрезок расположен целиком правее второго, то есть $$ \frac{7}{3}a - \frac{1}{3} \gt -\frac{5}{7}a + \frac{1}{7} $$ либо второй отрезок находится целиком правее первого, значит $$ -\frac{5}{7}a - \frac{1}{7} \gt \frac{7}{3}a + \frac{1}{3} $$

Поскольку нам не нужно ни первое, ни второе, в обоих неравенствах следует заменить знак $\gt$ знаком $\leqslant$. Таким образом приходим к следующей системе неравенств: $$ \begin{cases} \dfrac{7}{3}a - \dfrac{1}{3} \leqslant -\dfrac{5}{7}a + \dfrac{1}{7} \\ -\dfrac{5}{7}a - \dfrac{1}{7} \leqslant \dfrac{7}{3}a + \dfrac{1}{3} \end{cases} \quad \Leftrightarrow \quad \begin{cases} a \leqslant \dfrac{5}{32} \\ a \geqslant -\dfrac{5}{32} \\ \end{cases} $$

Ответ: $a \in [-\frac{5}{32}, \frac{5}{32}]$ или $|a| \leqslant 0,15625$.

4.5 Найти площадь множества точек $z$ комплексной плоскости, удовлетворяющих неравенству $|z+3+2i| + |z-5-4i| \lt 12$

Заданное неравенство можно переписать в виде: $$ |z-(-3-2i)|+|z-(5+4i)| \lt 12 \label{eq:4.5.1}\tag{4.5.1} $$

Пусть $p=-3-2i$, $q=5+4i$, $P$ и $Q$ точки комплексной плоскости,соответствующие этим числам. Тогда выражение в левой части $\eqref{eq:4.5.1}$ является суммой расстояний от точки, соответствующей числу $z$ до точек $P$ и $Q$. Таким образом задача свелась к следующей: Найти множество точек, сумма расстояний от которых до точек $P$ и $Q$ меньше $12$. Таким множеством является внутренность эллипса, фокусами которого являются точки $P$ и $Q$, а длина большой оси равна $2a=12$.

Как известно, площадь эллипса находится по формуле $S = \pi a b$, где $a$ и $b$ — длины полуосей. Длина большой полуоси нам известна: $a=6$.

Для нахождения длины малой полуоси находим фокусное расстояние: $$ 2c = |p - q| = |(-3-5)+(-2-4)i| = |8+6i| = \sqrt{8^2 + 6^2} = 10 \quad \Rightarrow \quad c=5 $$

Таким образом длина малой полуоси $b = \sqrt{a^2 - c^2} = \sqrt{36-25} = \sqrt{11}$

Находим, наконец, площадь эллипса: $S=\pi \cdot 6 \cdot \sqrt{11} = 6\pi\sqrt{11} \approx 62,5$

4.6Определить, при каких вешественных значениях $a$:
   а) неравенство $3-|x-a| \gt x^2$   имеет хотя бы одно отрицательное решение
   b) неравенство $2 \gt |x+a|+x^2$   имеет хотя бы одно положительное решение

Экономфак МГУ 1977. Источник: «С.Овчинников, И.Шарыгин. Решение неравенств с модулем. Квант №2, 1979 г». К сожалению, в оригинале нет ни решения ни даже ответа.

Неравенство пункта a) приводится к виду $|x-a| \lt 3-x^2$, в случае пункта b) получаем $|x+a| \lt 2-x^2$. В последнем неравенстве сделаем подстановку: $t=-x$. Тогда положительному значению $x$ соответствует отрицательное значение $t$, а само неравенство приобретает вид: $|t-a| \lt 2-t^2$.

Таким образом обе задачи сводятся к следующей: для заданного положительного $c$ найти значения $a$, при которых неравенство $|x-a| \lt c-x^2$ имеет хотя бы один отрицательный корень.

Приступим к решению этой задачи.

График функции $f(x)=|x-a|$ состоит из двух полупрямых: правая полупрямая: $f_r(x)=x-a$, левая полупрямая: $f_l(x)=a-x$. Точка излома имеет координаты $(a, 0)$, остальные точки лежат в верхней полуплоскости. График пересекает ось ординат в точке $(0, |a|)$. График функции $g(x)=c-x^2$ является повернутой вниз параболой, он симметричен относительно оси ординат и пресекает эту ось в точке $(0,c)$.

При достаточно большом $a$ графики не пресекаются, при этом график $f(x)$ находится выше $g(x)$, так что корней нет. По мере уменьшения $a$ графики начнут пресекаться, но только в первом в квадранте, тогда как во втором квадранте по-прежнему график $f(x)$ расположен выше $g(x)$.

Пересечение во втором квадранте наступит после того, как графики пресекутся на оси ординат. В этом случае $f_l(0) = g(0) = c$, то есть $a=c$. После этого часть графика $f(x)$ будет находиться ниже графика $g(x)$ во втором квадранте, так что отрицательные корни появятся. Таким образом получили верхнюю границу существования отрицательных корней: $a \lt c$.

При дальнейшем уменьшении $a$ графики снова перестанут пересекаться и график $f(x)$ снова окажется выше $g(x)$. Произойдет это после того, как правая полупрямая коснется графика функции $g(x)$, при этом дискриминант квадратного трехчлена $f_r(x)-g(x)$ равен нулю. В дальнейшем дискриминант станет отрицательным и корней не будет. Выразим значение дискриминанта через $a$. Имеем: $$ f_r(x) - g(x) = x-a - (c-x^2) = x^2 + x - (a+c) \quad \Rightarrow \quad D=1+4(a+c) $$

Решая неравенство $1+4(a+c) \gt 0$ (поскольку исходное неравенство для $x$ является строгим, дискриминант должен быть строго положительным) находим: $a \gt -(c+\frac{1}{4})$.

Итак окончательно: $-\left(c+\dfrac{1}{4}\right) \lt a \lt c$.

Подставляя $c=3$ и $c=2$, получаем ответы:

Ответы: a) $а \in (-3,25; -3)$; b) $a \in (-2,25; 2)$.

4.7Докажите, что если для вещественных чисел $a$, $b$ и $c$ выполняются неравенства $|a-b| \geqslant |c|$, $|b-c| \geqslant |a|$, $|c-a| \geqslant |b|$, то хотя бы одно из этих чисел равно сумме двух других.

Московская математическая олимпиада, 1996г.

Возводя первое неравенство в квадрат и перенося правую часть влево, получим: $(a-b)^2 - c^2 = 0$, или $$ (a-b-c)(a-b+c) \geqslant 0 $$

Аналогично для остальных двух неравенств: $$ (b-c-a)(b-c+a) \geqslant 0 \\ (c-a-b)(c-a+b) \geqslant 0 $$

Ввиду знаков $\geqslant$ обе части каждого из неравенств неотрицательны, что позволяет их перемножить. Получаем: $$ (a-b-c)(a-b+c)(b-c-a)(b-c+a)(c-a-b)(c-a+b) \geqslant \label{eq:4.7.1}\tag{4.7.1} $$

Так много сомножителей, и хоть бы один повторился! Хотя нет, по сути дела дела они повторяются, только с разными знаками. Поэтому разобьем их на пары, в каждой из которых сомножители отличаются только знаком. Перемножив сомножители каждой пары, получим: $$ (a-b-c)(c-a+b) = -(c+b-a) \cdot (c+b-a) = -(c+b-a)^2 \\ (a-b+c)(b-c-a) = (a+c-b) \cdot -(a+c-b) = -(a+c-b)^2 \\ (b-c+a)(c-a-b) = (a+b-c) \cdot -(a+b-c) = -(a+b-c)^2 $$ Таким образом левая часть неравенства $\eqref{eq:4.7.1}$ равна в $(-1)^3 (c+b-a)^2 (a+c-b)^2 (a+b-c)^2$ или $-(c+b-a)^2(a+c-b)^2(a+b-c)^2$, так что: $$ -(c+b-a)^2(a+c-b)^2(a+b-c)^2 \geqslant 0 $$ или $$ (c+b-a)^2(a+c-b)^2(a+b-c)^2 \leqslant 0 $$

Так как квадрат числа может быть неположительным только будучи равным нулю, хотя один из сомножителей должен быть нулем. Таким образом должно иметь место хотя бы одно из равенств: $a=b+c$, $b=a+c$, $c=a+b$. Это значит, что хотя бы одно из чисел равно сумме двух остальных.

4.8Докажите, что если разность между наибольшим и наименьшим из $n$ вещественных чисел $a_1$, $a_2$, ... $a_n$ равна $d$   (т.е. $d=\max\limits_{i \lt j}|a_i-a_j|$), a $s$ — сумма модулей всех попарных разностей этих чисел ($s=\sum\limits_{i \lt j}{|a_i-a_j|}$), то $(n-1)d \leqslant s \leqslant \frac{n^2}{4}d$.

Квант №7 1970, задача М13 (Одна из самых ранних задач журнала). Предлагается решение (Квант №7 1970, стр. 32) автора задачи, пожелавшего остаться неизвестным.

Без ограничения общности можно считать, что числа занумерованы в порядке неубывания: $a_1 \leqslant a_2 \leqslant \dots \leqslant a_n$.

Обозначим через $d_k$ разность между $a_k$ и $a_{k+1}$:   $d_k = a_{k+1}-a_k$. В таком случае

Тогда: $$ d = d_1 + d_2 + ... d_k = \sum\limits_{k=1}^{n-1}{d_k} \label{eq:4.8.1}\tag{4.8.1} $$

Подсчитаем теперь число $s$. Для этого заметим, что если $i \lt j$, то $$ |a_i - a_j| = a_j - a_i = d_i + d_{i+1} + \dots + d_{j-1} $$

Легко заметить, что $d_k$ участвует в суммировании для $|a_i-a_j|$ тогда и только тогда, когда $i \leqslant k$, а $j \geqslant k+1$. Паруя каждое $i=1,2 \dots k$ с каждым $j = k+1,k+2,\dots n$ получаем $k(n-k)$ различных длин $|a_i-a_j|$, в которых участвует $d_k$. Таким образом, сумма всех длин равна: $$ s = \sum\limits_{k=1}^{n-1}{k(n-k)d_k} \label{eq:4.8.2}\tag{4.8.2} $$

Осталось доказать следующее неравенство: $$ n-1 \leqslant k(n-k) \leqslant \frac{n^2}{4} \label{eq:4.8.3}\tag{4.8.3} $$

В самом деле: $$ \begin{array}{l} k(n-k) - (n-1) = kn-k^2-n+1 = n(k-1)-(k^2-1) = (n-k+1)(k-1) \geqslant 0 \quad (\text{ввиду}\; 1\leqslant k \leqslant n-1) \\ \dfrac{n^2}{4} - k(n-k) = \dfrac{n^2-4nk+4k^2}{4} = \dfrac{(n-2k)^2}{4} \geqslant 0 \end{array} $$

Применяя неравенство $\eqref{eq:4.8.3}$ к выражению для $s$ $\eqref{eq:4.8.2}$, получаем: $$ \sum\limits_{k=1}^{n-1}{(n-1)d_k} \leqslant \sum\limits_{k=1}^{n-1}{k(n-k)d_k} \leqslant \sum\limits_{k=1}^{n-1}{d\frac{n^2}{4}d_k} \\ (n-1)\sum\limits_{k=1}^{n-1}{d_k} \leqslant s \leqslant \dfrac{n^2}{4}\sum\limits_{k=1}^{n-1}{d_k} $$

Наконец, учитывая $\eqref{eq:4.8.1}$, получаем: $(n-1)d \leqslant s \leqslant \frac{n^2}{4} \,d$, что и требовалось.

Часть двойного неравенства обращается в равенство, когда соответствующая часть $\eqref{eq:4.8.3}$ обращается в равенство.

Так, для обращения левого неравенства в равенство требуется $n-1 = k(n-k)$, для чего в свою очередь, как следует из доказательства неравенства, необходимо либо $k=1$, либо $k=n-1$, другими словами, все $a_i$, кроме $a_1$ или $a_n$ должны быть одинаковы. Действительно, если, например, $a_1 \lt a_2 = a_3 = \dots = a_n$, то $d=a_2 - a_1$, разности вида $|a_1 - a_i|$, где $i=2,3, \dots n$ (таковых $(n-1)$ штук) равны $d$, остальные — нули, так что действительно $s=(n-1)d$.

Приглядевшись к доказательству правого неравенства из $\eqref{eq:4.8.3}$ можно заметить, что для его обращения в равенство необходимо $n=2k$ или $k=\frac{n}{2}$, что возможно лишь при четном $n$. В этом случае берем $a_1 = a_2 = \dots = a_m \lt a_{m+1} = a_{m+2} = \dots = a_n$, где $m=\frac{n}{2}$, что разбивает множество {$a_i$} на 2 группы по $m$ в каждой, при этом $|a_i-a_j| = d$, для чисел из разных групп и нулю для чисел из одной группы, так что $s= m^2\,d = \frac{n^2}{4}d$. При нечетном $n$ группы получаются неравными: в одной $\frac{n-1}{2}$ элементов, в другой $\frac{n+1}{2}$. В этом случае максимально возможное значение $s$ (что нетрудно доказать строго) равно $\frac{n-1}{2} \cdot \frac{n+1}{2} d$ или $\frac{n^2-1}{4}d$, поэтому при нечетном $n$ правое неравенство можно усилить.

4.9Докажите, что если множество вещественных чисел $$ \begin{matrix} a_{11},\; a_{12},\; \dots, \; a_{1n}\\ a_{21},\; a_{22},\; \dots, \; a_{2n}\\ .\;.\;.\;.\;.\\ a_{n1},\; a_{n2},\; \dots, \; a_{nn} \end{matrix} $$ для некоторого положительного $M$ удовлетворяет неравенствам $$ \sum\limits_{i=1}^{n}|a_{i1}\cdot x_1 + a_{i2} \cdot x_2 + \dots + a_{in}\cdot x_n| \leqslant M \label{eq:4.9.1}\tag{4.9.1} $$ для любого набора $\{x_1,\dots, x_n\}$ из чисел, равных $\pm 1$   (другими словами   $|x_k|=1$,   $k=1,2,\dots, n$),   то справедлива оценка $$ |a_{11}|+|a_{22}|+\dots+|a_{nn}| \leqslant M $$

Математическая олимпиада Югославии, 1972г.

Согласно правилу произведения существует $2^n$ всевозможных наборов из $n$ чисел, равных $\pm 1$. (Впрочем, количество наборов не существенно для доказательства, так что сомневающиеся могут просто заменить $2^n$ на $Т$, и $2^{n-1}$ на $\frac{T}{2}$.)

Суммируя неравенства $\eqref{eq:4.9.1}$ по всем наборам, получаем: $$ \sum\limits_{\{x_1,\dots\,x_n\}} \sum\limits_{i=1}^{n}|a_{i1}\cdot x_1 + a_{i2} \cdot x_2 + \dots + a_{in}\cdot x_n| \leqslant 2^n\,M $$ или, после изменения порядка суммирования: $$ \sum\limits_{i=1}^{n} \sum\limits_{\{x_1,\dots\,x_n\}} |a_{i1}\cdot x_1 + a_{i2} \cdot x_2 + \dots + a_{in}\cdot x_n| \leqslant 2^n\,M \label{eq:4.9.2}\tag{4.9.2} $$

Рассмотрим внутреннюю сумму $$ S_i = \sum\limits_{\{x_1,\dots\,x_n\}} |a_{i1}\cdot x_1 + a_{i2} \cdot x_2 + \dots + a_{in}\cdot x_n| \label{eq:4.9.3}\tag{4.9.3} $$ для фиксированного $i$.

Суммирование здесь ведется по всем наборам $\{x_1,\dots\,x_n\}$, которые можно разбить на пары так, что в в каждой паре все элементы, кроме $i$-го совпадают. Таким образом, наборы соответствующие одной паре имеют вид $$ \{x_1,\dots,x_{i-1},\;-1\;,x_{i+1},\dots,x_n\} \quad \text{и} \quad \{x_1,\dots,x_{i-1},\;1\;,x_{i+1},\dots,x_n\}, $$ тогда как слагаемые такой пары равны $$ |a_{i1}\cdot x_1 + \dots + a_{i(i-1)}\cdot x_n \; \pm a_{ii} \; + a_{i(i+1)}\cdot x_{i+1} + \dots + a_{nn}x_n| $$

Обозначим через $P$ сумму всех элементов, кроме $i$-го: $$ P = a_{i1}\cdot x_1 + \dots + a_{i(i-1)}\cdot x_n + a_{i(i+1)}\cdot x_{i+1} + \dots + a_{nn}x_n $$

В таком случае слагаемые приобретают вид: $|P+a_{ii}|$   и   $|P-a_{ii}|$, так что, используя «модифицированное» неравенство треугольника $|a-b|\leqslant |a|+|b|$ (частный случай неравенства (1.3.6)), сумму одной пары можно оценить снизу: $$ |P + a_{ii}| + |P-a_{ii}| \geqslant |(P + a_{ii})-(P - a_{ii})| = 2|a_{ii}| $$

Учитывая, что имеется $2^{n-1}$ таких пар (в два раз меньше, чем количество наборов), получаем нижнюю оценку для $S_i$, определенного в $\eqref{eq:4.9.3}$ $$ S_i \geqslant 2^{n-1}\cdot 2|a_{ii}| = 2^n |a_{ii}| \label{eq:4.9.4}\tag{4.9.4} $$

Применяя оценку $\eqref{eq:4.9.4}$ к неравенству $\eqref{eq:4.9.2}$, получаем: $$ 2^n\,M \geqslant \sum\limits_{i=1}^{n} |a_{i1}\cdot x_1 + a_{i2} \cdot x_2 + \dots + a_{in}\cdot x_n| = \sum\limits_{i=1}^{n} S_i \geqslant 2^n \sum\limits_{i=1}^{n} |a_{ii}| $$

Таким образом: $$ |a_{11}| + |a_{22}| + \dots + |a_{nn}| = \sum\limits_{i=1}^{n} |a_{ii}| \leqslant M, $$ что и требовалось доказать.

Кстати, данное доказательство подходит и для комплексных $a_{ij}$.

 

Описание и условия задач

Решения задач части 1

Решения задач части 2

Решения задач части 3

Решения задач части 4

Описание и условия задач

Решения задач части 1

Решения задач части 2

Решения задач части 3

Решения задач части 4

 

3.1Построить график функции $y=|\sqrt{|x+2|}-1|$

Построение состоит из следующих этапов

1. $y=\sqrt{|x|}$. Строим график функции $y=\sqrt{x}$ (он расположен только в первом квадранте), и дополняем его собственным отражением относительно оси ординат.
2. $y=\sqrt{|x+2|}$. Сдвигаем построенный график на 2 единицы влево.
3. $y=\sqrt{|x+2|}-1$. Сдвигаем построенный график на 2 единицы влево.
4. $y=|\sqrt{|x+2|}-1|$. Заменяем часть графика, лежащей в нижней полуплоскости ее отражением относительно оси абсцисс.

1.   $\sqrt{|x|}$		2.   $\sqrt{|x|} \quad \rightarrow \quad \sqrt{|x+2|}$
3.   $\sqrt{|x+2|} \quad \rightarrow \quad \sqrt{|x+2|}-1$		4.   $\sqrt{|x+2|}-1 \quad \rightarrow \quad |\sqrt{|x+2|}-1|$

 

3.2Построить график функции $y=\frac{|x+2|}{|x-1|}$

В данном случае уравнение функции следует подготовить: $$ y = \left| \dfrac{x+2}{x+1} \right| = \left| 1 + \dfrac{1}{x+1} \right| $$

Теперь понятно, что требуется построить график функции $y=\frac{1}{x}$ (это гипербола), сдвинуть на единицу влево и единицу вверх, а затем зеркально отразить его часть в нижней полуплоскости относительно оси абсцисс.

 

3.3Построить график функции $y=|2x+1|-|x+5|+|x+1|-|2x-5|$

Так как аргумент $x$ всюду находится в первой степени, график состоит из отрезков между точками излома и полупрямых по краям.

Выпишем точки излома в порядке возрастания: $-5$, $-1$, $-0,5$, $2,5$. Находим значения функции в точках излома: $$ \begin{array}{l} f(-5) = 11 + 0 + 6 - 15 = -2 \\ f(-1) = 1 - 4 + 0 - 7 = -10 \\ f(-0,5) = 0 - 4,5 + 0,5 - 6 = -10 \\ f(2,5) = 6 - 7,5 + 3.5 - 0 = 2 \end{array} $$

Для построения графика в крайних полуинтервалах $(-\infty, -5]$ и $[2,5, \; +\infty)$ выберем по одной точке в каждом интервале и вычислим значения функции в этих точках: $$ \begin{array}{l} f(-7) = 13 - 2 + 6 - 19 = -2 \\ f(4) = 9 - 9 + 5 - 3 = 2 \end{array} $$

График функции показан на чертеже. Как видим, функция постоянна в промежутках $(-\infty, \; -5]$, $[-1, \; -0,5]$ и $[2,5, \; +\infty)$

 

3.4Построить график функции $y=x^2-5|x-1|+5$

Воспользуемся методом интервалов.

Полагая $x \geqslant 1$ находим: $f(x) = x^2-5x+10$. Дискриминант функции равен $25-50=-15\lt 0$, функция положительна на всей числовой оси, координаты вершины $(\frac{5}{2}, \frac{15}{4})$, ось симметрии $x=\frac{5}{2}=2,5$. При $x=0$ находим $y=10$. Такое же значение имеет функция в симметричной точке с $x=5$. В точке излома $x=1$, $y=6$. Строим график и выбираем его часть, с $x \geqslant 1$.

При $x \lt 1$ получаем $f(x)=x^2+5x$. Функция имеет нули при $x=0$ и $x=-5$, координаты вершины: $(-\frac{5}{2}, -\frac{25}{4})$. В точке излома $x=1$, $y=6$, совпадение значений в точке излома согласуется с непрерывностью функции. Строим график и выбираем его часть, с $x \lt 1$.

В результате получаем следующее:

3.5Построить множество точек координатной плоскости, удовлетворяющих неравенству $|y+1|+|x-4| \lt x$.

Перепишем заданное неравенство в виде: $$ |y+1| \lt x-|x-4| \label{eq:3.5.1}\tag{3.5.1} $$

Для существования решения правая часть должна быть положительной. Таким образом: $$ |x-4| \lt x \quad \Leftrightarrow \quad -x \lt x-4 \lt x \quad \Leftrightarrow \quad -2x \lt -4 \lt 0 \quad \Leftrightarrow \quad x \gt 2 $$

Таким образом неравенство имеет решение при $x \gt 2$.

Введя обозначение $f(x)=x-|x-4|$, неравенство $\eqref{eq:3.5.1}$ можно переписать в виде: $$ -f(x) \lt y+1 \lt f(x) $$ или $$ -f(x)-1 \lt y \lt f(x)-1 $$

Отсюда вытекает следующий план действия:

1. Строим график функции $f(x)=x-|x-4|$ на полуинтервале $[2, +\infty)$
2. Зеркально отображаем построенный график относительно оси абсцисс, что дает график функции $-f(x)$
3. Сдвигаем оба графика на единицу вниз. Искомое множество располагается между графиками, исключая линии графиков.

Для построения графика функции $f(x)$ рассмотрим два промежутка для $x$:
$$ \begin{array}{l} x \in (2,4): \quad f(x) = x + x - 4 = 2x-4 \\ x \in [4, +\infty): \quad f(x) = x -x + 4 = 4 \end{array} $$

Находим значения функции в особых точках: $f(2)=0$, $f(4)=4$, значение для $x=4$ согласуется с непрерывностью функции $f(x)$.

Построение множества точек приведено на чертеже.

 

3.6Построить множество точек координатной плоскости, удовлетворяющих неравенству $x^2+y^2+x|x|+y|y| \gt 8$.

Применим метод интервалов и рассмотрим вид неравенства в каждом квадранте:

Квадрант	Интервалы $x$ и $y$	Неравенство
I	$\begin{cases} x \geqslant 0 \\ y \geqslant 0 \end{cases}$	$x^2+y^2 \gt 4$ внешность окружности радиуса 2
II	$\begin{cases}x \lt 0 \\ y \geqslant 0\end{cases}$	$y^2 \gt 4\quad\Leftrightarrow\quad y\gt 2 $ выше прямой $y=2$
III	$\begin{cases}x \lt 0 \\y \lt 0\end{cases}$	$0 \gt 8$ невозможно
IV	$\begin{cases}x \geqslant 0 \\y \lt 0\end{cases}$	$x^2 \gt 4\quad\Leftrightarrow\quad x\gt 2$ правее прямой $x=2$

Искомое множество точек показано на чертеже.

 

3.7Решить уравнение в области комплексных чисел: $|z-2+3i| = |4+i\sqrt{3}|$.

Правая часть является константой. Вычислим ее:

$$ |4+i\sqrt{3}| = \sqrt{4^2+3^2} = 5 $$

Таким образом заданное уравнение переписывается в виде $$ |z-(2-3i)| = 5 $$ и его можно сформулировать следующим образом: «найти множество точек комплексной плоскости, расстояние от которых до точки, соответствующей числу $2-3i$ равно 5. Таким множеством является окружность с радиуса 5 с центром в точке $(2,-3)$

3.8Решить неравенство в области комплексных чисел: $||z-2|-(7+4i)| \leqslant 5$.

Число под внешним знаком модуля можно представить в виде $$ A = (|z-2|-7) - 4i $$

Так как $|z-2|$ — вещественное число, действительной частью $А$ является $|z-2|-7$, тогда как $(-4)$ является его мнимой частью. Таким образом: $$ |A| = \sqrt{(|z-2|-7)^2+16} $$ что позволяет переписать заданное неравенство в виде: $$ (|z-2|-7)^2+16 \leqslant 25 $$ откуда $$ ||z-2|-7| \leqslant 3 \quad \Leftrightarrow \quad -3 \leqslant |z-2|-7 \leqslant 3 \quad \Leftrightarrow \\ 4 \leqslant |z-2| \leqslant 10 $$

Искомое множество точек расположено между концентрическими окружностями радиусами 4 и 10 с центром в точке $(2,0)$. Окружности включаются, так как неравенства нестрогие.

3.9Решить уравнение в области комплексных чисел: $z^2-5|z|+6 = 0$.

Запишем уравнение в виде $$ z^2 = 5|z| - 6 $$ откуда следует, что $z^2$ — вещественное число.

Пусть $z=a+bi$. Тогда $$ z^2 = a^2 + 2abi + b^2i^2 = (a^2-b^2) + 2abi $$

Так как мнимая часть $2ab$ равна нулю, хотя бы одно из чисел $a$ и $b$ должно быть нулем, так что $z=a$ или $z=bi$

Если $z=a$, то $z^2 = a^2 = |a|^2$, $|z|=|a|$, Это приводит к уравнению $|a|^2 - 5|a| + 6 = 0$, решая которое находим возможные значения $|a|$: 2 и 3. Таким образом $z_{1,2} = \pm 2$, $z_{3,4} = \pm 3$.

Если $z=bi$, то $z^2 = -b^2 = -|b|^2$, $|z|=|b|$. В этот раз приходим к уравнению $|b|^2 + 5|b| - 6 = 0$, корни которого 1 и (-6). Так как $|b|$ — неотрицательное число, то $|b|=1$, откуда $z_{5,6} = \pm i$.

Ответ: $z_1=2$, $z_2=-2$, $z_3=3$, $z_4=-3$, $z_5=i$, $z_6=-i$. Как видим, в этом случае, несмотря на наличие модуля, уравнение имеет конечное количество решений.

 

Описание и условия задач

Решения задач части 1

Решения задач части 2

Решения задач части 3

Решения задач части 4

Описание и условия задач

Решения задач части 1

Решения задач части 2

Решения задач части 3

Решения задач части 4

 

2.1Решить в области вещественных чисел: $||5-2x|-1| = 4$.

Преобразуем заданное уравнение: $$ \begin{array}{l} |5-2x|-1 = \pm 4 \; \Leftrightarrow \\ |5x-2x| = 1 \pm 4 \end{array} $$

Так как абсолютная величина не может быть отрицательной, значение $1-4=-3$ отбрасывается. Таким образом $$ \begin{array}{l} |5-2x| = 5 \; \Leftrightarrow \\ 5-2x = \pm 5 \; \Leftrightarrow \\ x = \dfrac{5 \pm 5}{2} \end{array} $$

Ответ: $x_1 = 0$,   $x_2 = 5$.

2.2Решить в области вещественных чисел: $|sin\,x| = cos\,x$.

Из многочисленных способов решения этого уравнения покажем два.

Первый способ. В отличие от предыдущего уравнения правая часть не является константой. Поэтому, заменяя данное уравнение уравнением $sin\,x = \pm cos\,x$ мы приобретаем лишние корни, соответствующие уравнению $|sin\,x| = -cos\,x$. Таким образом, от значений $x$ с отрицательным косинусом придется избавиться.

Имея это в виду, преобразуем полученное уравнение: \begin{array}{l} sin\,x = \pm cos\,x \; \Leftrightarrow \; sin\,x \pm cos\,x = 0 \; \Leftrightarrow \\ \sqrt{2}\, sin(x \pm \dfrac{\pi}{4}) = 0 \; \Leftrightarrow \; x \pm \dfrac{\pi}{4} = \pi k \quad k=0,\pm1,\pm2 \dots \end{array}

Таким образом, $$ x = \pm \dfrac{\pi}{4} + \pi k \quad k=0,\pm1,\pm2 \dots $$ что в промежутке $\left[-\frac{\pi}{2}, \frac{3\pi}{2}\right)$ дает следующие значения $x$: $-\frac{\pi}{4}$, $\frac{\pi}{4}$, $\frac{3\pi}{4}$, $\frac{5\pi}{4}$.   Неотрицательный косинус имеет место при $x = -\frac{\pi}{4}$ и $x=\frac{\pi}{4}$.

Ответ: $x= \pm \frac{\pi}{4} + 2\pi k \quad k=0,\pm1,\pm2 \dots$.

Второй способ. Возводим в квадрат. При этом приобретаются лишние корни с отрицательным косинусом. $$ sin^2 x = cos^2 x $$

Подстановка $sin^2 x = 1 - cos^2 x$, позволяет найти $cos^2x$: $$ cos^2 x = \dfrac{1}{2} $$

Поскольку $cos\,x$ неотрицателен, $cos\,x = \dfrac{\sqrt{2}}{2}$.

Ответ: $x= \pm \frac{\pi}{4} + 2\pi k \quad k=0,\pm1,\pm2 \dots$.

2.3Решить в области вещественных чисел: $|sin\,x| \gt cos\,x$.

По сравнению с предыдущей задачей изменился только знак: равенство стало неравенством. Однако подход принципиально отличается.

При $cos\,x \lt 0$ неравенство заведомо выполняется.

В случае $cos\,x \geqslant 0$ обе части неравенства неотрицательны, так что его можно без боязни возводить в квадрат: $$ sin^2 x \gt cos^2 x $$

Знакомая подстановка $sin^2 x = 1 - cos^2 x$ приводит к неравенству $$ cos^2 x \lt \dfrac{1}{2} $$ и поскольку $cos\,x$ снова неотрицателен, то $0 \leqslant cos\,x \lt \dfrac{\sqrt{2}}{2}$

Объединив полученное неравенство с неравенством $cos\,x \lt 0$, получаем: $cos\,x \lt \dfrac{\sqrt{2}}{2}$, откуда находим значения $x$.

Ответ: $\frac{\pi}{4} + 2\pi k \lt x \lt \frac{7\pi}{4} + 2\pi k$,   $k=0, \pm1, \pm2, \dots$

2.4Решить в области вещественных чисел: $|x^4-x^2-5| = ||x^4-4|-x^2-1|$.

Так как корни многочленов найти не просто, применим хитрый способ. Из второго неравенства треугольника следует: $$ |x^4-x^2-5| = |(x^4-4)-(x^2+1)| \geqslant ||x^4-4|-|x^2+1|| $$

Поскольку выражение $x^2+1$ заведомо положительно, $|x^2+1|=x^2+1$, откуда получаем $$ |x^4-x^2-5| \geqslant ||x^4-4|-x^2-1| $$ что совпадает с заданным уравнением «с точностью до знака».

Требуется полученное неравенство обратить в равенство, для чего необходимо и достаточно, чтобы среди чисел, $(x^4-4)$ и $(x^2+1)$ был нуль, или числа были одинакового знака. Поскольку число $(x^2+1)$ может быть только положительным, всё зависит от $(x^4-4)$: оно должно быть или нулем, или положительным: $$ x^4 - 4 \geqslant 0 \quad \Leftrightarrow \quad x^2 \geqslant 2 \quad \Leftrightarrow \quad |x| \geqslant \sqrt{2} $$

Ответ: $x \in (-\infty, -\sqrt{2}] \cup [\sqrt{2}, +\infty)$.

2.5Решить в области вещественных чисел: $|x-2|+|x-1|+|x|+|x+1|+|x+2| \leqslant 6$

Источник: МЦМНО (problems.ru) задача 35150 В оригинале равенство вместо неравенства.

Первый способ. Обозначим функцию в левой части через $f(x)$: $$ f(x)=|x-2|+|x-1|+|x|+|x+1|+|x+2| $$

Точки излома функции: $x=0, \pm1, \pm2$, однако, поскольку $f(x)$ — четная функция ($f(-x)=f(x)$), достаточно рассмотреть неотрицательные значения $x$.

Находим значения $f(x)$ в точках излома: $$ \begin{array}{l} f(0) = 2 + 1 + 0 + 1 + 2 = 6 \\ f(1) = 1 + 0 + 1 + 2 + 3 = 7 \\ f(2) = 0 + 1 + 2 + 3 + 4 = 10 \end{array} $$

Так как аргумент $x$ всюду появляется в первой степени, график функции между точками излома является отрезком прямой. Ввиду $f(2) \gt f(1) \gt f(0)$ функция $f(x)$ монотонно возрастает на отрезке [0,2], поэтому $f(x) \gt f(0) = 6$ при $x \in (0,2]$. Также $f(x) \gt 6$ на интервале $(2, +\infty)$, поскольку в противном случае линейная функция на этом бесконечном интервале была бы убывающей и достигла отрицательных значений, что невозможно, ввиду того, что $f(x)$ — сумма абсолютных величин. Таким образом нуль — единственное значение аргумента, где $f(x) \leqslant 6$.

Ответ: $x=0$.

Второй способ. Воспользуемся «модифицированным неравенством треугольника» (частный случай неравенства (1.3.6)): $$ |a-b| \leqslant |a| + |b| $$

Имеем: $$ |(x+2)-(x-2)| \leqslant |x-2| + |x+2| $$ или $$ |x-2| + |x+2| \geqslant 4 $$

Аналогично: $$ |x-1| + |x+1| \geqslant 2 $$

И уж конечно $$ |x| \geqslant 0 $$

Складывая последние три неравенства, получаем неравенство: $$ |x-2|+|x-1|+|x|+|x+1|+|x+2| \geqslant 6 $$ которое отличается от заданного неравенства только направлением знака. В таком случае неравенства могут быть совместными только при наличии равенства, для чего необходимо, чтобы каждое из трех сложенных неравенств было равенством. В частности $|x| = 0$, то есть $x=0$. Подставляя значение $x=0$ в заданное неравенство убеждаемся в том, что оно верно.

Ответ: $x=0$.

2.6Решить в области вещественных чисел: $x^2\cdot 2^{x+1}+2^{|x-3|+2} = x^2\cdot 2^{|x-3|+4}+2^{x-1}$.

Вступительные экзамены в мехмат МГУ 1961г.

По-видимому здесь нет ничего лучше рассмотрения промежутков. Благо у нас их всего два.

Если $x \geqslant 3$, то $|x-3| = x-3$, что приводит ... $$ x^2\cdot 2^{x+1} + 2^{x-1} = x^2\cdot 2^{x+1} + 2^{x-1} $$ к тождеству! Таким образом все точки полуинтервала $[3,+\infty)$ удовлетворяют уравнению.

Обратимся к менее тривиальному случаю $x \lt 3$, при котором $|x-3|=3-x$, так что получается: $$ x^2\cdot 2^{x+1} + 2^{5-x} = x^2\cdot 2^{7-x} + 2^{x-1} $$

Когда других идей нет, остается разложение на множители. Пробуем это сделать: $$ x^2\cdot 2^{x+1} - x^2\cdot 2^{7-x} + 2^{5-x} - 2^{x-1} = 0 \\ 2^2\,x^2\,(2^{x-1} - 2^{5-x}) - (2^{x-1} = 2^{5-x}) = 0 \\ (4x^2 - 1)(2^{x-1} - 2^{5-x}) = 0 $$

Уравнение распадается на два: $$ \begin{array}{l} 4x^2-1 = 0 \quad \Leftrightarrow \quad x=\pm\frac{1}{2} \\ 2^{x-1} = 2^{5-x} \quad \Leftrightarrow \quad x-1 = 5-x \quad \Leftrightarrow \quad x=3 \end{array} $$

Решение $x=3$ попадает в ранее рассмотренный промежуток $[3,+\infty)$.

Ответ: $x \in \{-0,5\} \cup \{0,5\} \cup [3,+\infty)$.

2.7Решить в области вещественных чисел: $\begin{cases}|x+y| = 1 \\ |x|+|y| = 3\end{cases}$

Первый способ. Так как обе части обоих уравнений системы заведомо неотрицательны, при возведении в квадрат лишние корни не приобретаются. Проделаем это: $$ \begin{cases} x^2+ 2xy + y^2 = 1\\ x^2+ 2|xy| + y^2 = 9 \end{cases} \label{eq:2.7.1}\tag{2.7.1} $$

Вычитая из первого уравнения системы $\eqref{eq:2.7.1}$ второе, получаем: $$ 2(xy - |xy|) = -8 \label{eq:2.7.2}\tag{2.7.2} $$

Если $xy \geqslant 0$, то $|xy| = xy$, что превращает $\eqref{eq:2.7.2}$ в ложное равенство $0=-8$. Поэтому $xy \lt 0$, так что $|xy| = -xy$, и из $\eqref{eq:2.7.2}$ находим: $xy = -2$, или $$ y = -\frac{2}{x} \label{eq:2.7.3}\tag{2.7.3} $$

Подстановка вo второе уравнение заданной системы дает: $$ |x| + \frac{2}{|x|} = 3 \quad \Leftrightarrow \quad |x|^2 - 3|x| + 2 = 0 $$

откуда находим: $x_{1,2} = \pm 1$,   $x_{2,3} = \pm 2$. Осталось для каждого $x$ найти $y$ из $\eqref{eq:2.7.3}$

Ответ: $(x,y)$:   $(1, -2)$,   $(-1, 2)$,   $(2, -1)$,   $(-2, 1)$.

Второй способ. Если $x$ и $y$ одного знака, или среди них есть нуль, то $|x+y|=|x|+|y|$, что приводит к несовместной системе $\begin{cases} |x|+|y| = 1 \\ |x|+|y|=3 \end{cases}$. Поэтому числа $x$ и $y$ разных знаков, так что, ввиду утверждения 1.3.4, $|x+y|=||x|-|y||$, и система выглядит так: $$ \begin{cases} ||x|-|y|| = 1 \\ |x|+|y| = 3 \end{cases} $$

В силу симметричности обоих уравнений относительно $x$ и $y$, будем считать, что $|x| \geqslant |y|$, а затем добавим симметричное решение. Таким образом получаем систему $$ \begin{cases} |x|-|y| = 1 \\ |x|+|y| = 3 \end{cases} $$ решая которую, находим: $|x|=2$,   $|y|=1$.

Учитывая, что $x$ и $y$ разных знаков, имеем $x= \pm 2$,   $y= \mp 1$. Симметричное решение: $x = \pm 1$,   $y = \mp 2$.

Ответ: $(x,y)$:   $(2, -1)$,   $(-2, 1)$,   $(1, -2)$,   $(-1, 2)$.

2.8Решить в области вещественных чисел: $\begin{cases}|x+3|+|y+1| = 4 \\ |x-1|+|y-3| = 5\end{cases}$

Аналитический способ

Решим методом интервалов. Вначале исследуем каждое уравнение в отдельности. Результаты запишем в таблицы:

$|x+3|+|y+1| = 4$
	$x \lt -3$	$x \geqslant -3$
$y \lt -1$	$\begin{array}{c} -x-3-y-1=4 \\ x+y=-8 \end{array}$	$\begin{array}{c} x+3-y-1=4 \\ x-y=2 \end{array}$
$y \geqslant -1$	$\begin{array}{c} -x-3+y+1=4 \\ x-y=6 \end{array}$	$\begin{array}{c} x+3+y+1=4 \\ x+y=0 \end{array}$

$|x-1|+|y-3| = 5$
	$x \lt 1$	$x \geqslant 1$
$y \lt 3$	$\begin{array}{c} -x+1-y+3=5 \\ x+y=-1 \end{array}$	$\begin{array}{c} x-1-y+3=5 \\ x-y=3 \end{array}$
$y \geqslant 3$	$\begin{array}{c} -x+1+y-3=5 \\ x-y=-7 \end{array}$	$\begin{array}{c} x-1+y-3=5 \\ x+y=9 \end{array}$

 

Теперь рассматриваем различные варианты:

$x \lt -3$	$y \lt -1$	$\begin{cases} x+y=-8 \\ x+y=-1 \end{cases}$   несовместна
	$-1 \leqslant y \lt 3$	$\begin{cases} x-y=-6 \\ x+y=-1 \end{cases} \quad \Leftrightarrow \quad \begin{cases} x=-3,5 \\ y=2,5 \end{cases}$   подходит
	$ y \geqslant 3$	$\begin{cases} x-y=-6 \\ x-y=-7 \end{cases}$   несовместна
$-3 \leqslant x \lt 1$	$y \lt -1$	$\begin{cases} x-y=2 \\ x+y=-1 \end{cases} \quad \Leftrightarrow \quad \begin{cases} x=0,5 \\ y=-1,5 \end{cases}$   подходит
	$-1 \leqslant y \lt 3$	$\begin{cases} x-y=0 \\ x+y=-1 \end{cases}$   несовместна
	$ y \geqslant 3$	$\begin{cases} x+y=0 \\ x-y=-7 \end{cases} \quad x=-3.5$   не удовлетворяет промежутку
$x \geqslant 1$	$y \lt -1$	$\begin{cases} x-y=2 \\ x-y=3 \end{cases}$   несовместна
	$-1 \leqslant y \lt 3$	$\begin{cases} x+y=0 \\ x-y=3 \end{cases} \quad y=-1,5$   не удовлетворяет промежутку
	$ y \geqslant 3$	$\begin{cases} x+y=0 \\ x+y=9 \end{cases}$   несовместна

 

Ответ: $(x,y)$: $(-3,5; 2,5)$,   $(0,5; -1,5)$

Графический способ

Как выяснится чуть позже (задача 4.2) множеством точек координатной плоскости, удовлетворяющих равенству $|x|+|y|=c$ ($c \gt 0 $) является квадрат с вершинами в точках $(c,0)$, $(0,c)$, $(-c,0)$ и $(0,-c)$. В случае равенства $|x+a|+|y+b|=c$ квадрат следует сдвинуть вдоль оси абсцисс на $|a|$ единиц влево (при $a \gt 0$) или вправо (при $a \lt 0$), а также на $|b|$ единиц вверх (при $b \gt 0$) или вниз (при $b \lt 0$).

Таким образом получаем квадраты, изображенные на чертеже, пересечения которых дают требуемые решения.

Ответ: $(x,y)$: $(-3,5; 2,5)$,   $(0,5; -1,5)$

2.9Решить в области вещественных чисел: $|\sqrt{2}|x|-1| \cdot \log_2{(2-2x^2)} \geqslant 1$

Факультет эконом. кибернетики МГУ. Вступительный экзамен 1965г. На этот раз кибернетикам в самый раз, несмотря на то, что в то время не было ни персональных компьютеров, ни даже графических калькуляторов.☺️ Решение авторов задачи мне неизвестно, хотя очень хотелось бы взглянуть на него.

Так как левая часть неравенства обязана быть положительной, то учитывая $|\sqrt{2}|x|-1| \geqslant 0$, необходимо: $$ \log_2{(2-2x^2)} \gt 0 \quad \Leftrightarrow \quad 2-2x^2 \gt 1 \quad \Leftrightarrow \quad |x| \lt \dfrac{1}{\sqrt{2}} $$

Отсюда $\sqrt{2}|x|-1 \lt 0$, поэтому $|\sqrt{2}|x| -1| = 1 - \sqrt{2}|x|$.

Таким образом заданное неравенство переписывается в виде: $$ (1-\sqrt{2}{x}) \cdot \log_2{(2-2x^2)} \geqslant 1 \label{eq:2.9.1}\tag{2.9.1} $$

Заметим, что $$ 1-\sqrt{2}{x} \leqslant 1 \label{eq:2.9.2}\tag{2.9.2} $$ кроме того, из тождественного неравенства $2-2x^2 \leqslant 2$ и монотонности логарифма следует: $$ \log_2{(2-2x^2)} \leqslant \log_2{2} = 1 \label{eq:2.9.3}\tag{2.9.3} $$

Перемножая неравенства $\eqref{eq:2.9.2}$ и $\eqref{eq:2.9.3}$ (что оправдано, поскольку было выяснено, что оба сомножителя в левой части $\eqref{eq:2.9.1}$ положительны), получаем: $$ (1-\sqrt{2}{x}) \cdot \log_2{(2-2x^2)} \leqslant 1 $$ которое отличается от неравенства $\eqref{eq:2.9.1}$ только противоположным знаком. Таким образом, обязано иметь место равенство, так что оба неравенства $\eqref{eq:2.9.2}$ и $\eqref{eq:2.9.3}$ должны обращаться в равенство. Из $\eqref{eq:2.9.2}$ находим $x=0$. При этом заданное неравенство действительно верно, а других подходящих значений $x$ быть не может.

Ответ: $x=0$.

2.10Решить в области вещественных чисел: $\dfrac{4}{|x+1|-2} \geqslant |x-1|$

Факультет психологии МГУ. Вступительный экзамен 1979г.

Если знаменатель левой части отрицателен, вся левая часть становится отрицательной, что приводит к заведомо ложному неравенству. Так как знаменатель не может быть нулевым, он должен быть положительным. Таким образом приходим к неравенству $|x+1| \gt 2$, откуда $$ x \in (-\infty, -3) \cup (1, +\infty) \label{eq:2.10.1}\tag{2.10.1} $$

Положительность знаменателя, позволяет умножить на него обе части неравенства, что после упрощений приводит к $$ |x^2-1| - 2|x-1| - 4 \leqslant 0 $$

Далее замечаем, что, ввиду $\eqref{eq:2.10.1}$, $|x| \gt 1$, откуда $x^2 - 1 \gt 0$, что приводит к дальнейшему упрощению неравенства: $$ x^2 - 2|x-1| - 5 \leqslant 0 $$

Теперь, когда перебор минимизирован до предела, можно наконец перейти к рассмотрению каждого из интервалов в $\eqref{eq:2.10.1}$:

1) Если $x \in (1, +\infty)$, то $x-1 \gt 0$, так что получаем следующую систему неравенств: $$ \begin{cases} x \gt 1 \\ x^2-2x-3 \geqslant 0 \quad \Leftrightarrow \quad -1 \leqslant x \leqslant 3 \end{cases} $$ откуда $1 \lt x \leqslant 3$ или $x \in (1,3]$.

2) Пусть теперь $x \in (-\infty, -3)$. Тогда $x \lt 1$, так что $|x-1| = 1-x$. Это приводит к следующей системе неравенств: $$ \begin{cases} x \lt -3\\ x^2+2x-7 \geqslant 0 \quad \Leftrightarrow \quad -1-\sqrt{8} \leqslant x \leqslant -1+\sqrt{8} \end{cases} $$

Настроение такое бодрое, что даже иррациональные числа его не могут испортить. Тем более, что здесь все довольно просто: $$ \begin{array}{l} -1+\sqrt{8} \gt -1 \gt -3 \\ -1-\sqrt{8} \lt -1-\sqrt{4} = -3 \end{array} $$

Таким образом, $-3 \in (-1-\sqrt{8}, -1+\sqrt{8})$, так что решение системы неравенств: $-1-\sqrt{8} \leqslant x \lt -3$ или $x \in [-1-2\sqrt{2}, -3)$.

Ответ: $x \in [-1-2\sqrt{2}, -3) \cup (1, 3]$.

Между прочим, решение авторов задачи настолько длинное, что на него можно было потратить всё экзаменационное время. (Всего задач было 5.) Уверен однако, что будущие психологи оказались прозорливее авторов и не стали тратить время попусту.

 

Описание и условия задач

Решения задач части 1

Решения задач части 2

Решения задач части 3

Решения задач части 4